SUMMARY
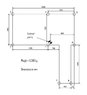
The discussion focuses on calculating the loads for a static fan weighing 6,060 kg, supported by a frame with specific cross-sectional dimensions of 200h x 90w. The problem is identified as statically indeterminate, with the need to account for the center of gravity and potential uneven load distribution due to variations in mount heights. The use of vibration mounts is suggested to help distribute the load, and it is emphasized that solving the problem involves managing a set of 11 simultaneous equations, which is impractical by hand. Consulting a structural engineer is recommended for compliance with building codes and accurate load calculations.
PREREQUISITES
- Understanding of static equilibrium and load distribution
- Familiarity with structural engineering principles
- Knowledge of vibration mounts and their applications
- Ability to solve simultaneous equations in engineering contexts
NEXT STEPS
- Research methods for calculating load distribution in statically indeterminate structures
- Learn about the properties and applications of vibration mounts in load-bearing scenarios
- Study the principles of static equilibrium in mechanical systems
- Consult resources on structural engineering codes and standards relevant to heavy equipment
USEFUL FOR
Structural engineers, mechanical engineers, and anyone involved in the design and analysis of load-bearing structures, particularly those working with heavy static loads like large fans.