Calculating Loss of Mechanical Energy in Bouncing Ball Experiment

[amanda.ka]

Homework Statement

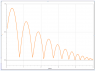
I did an experiment in which I bounced a ball under a motion sensor. From that I got a generated graph on the computer in the shape of a parabola. The max height of the ball at each interval was also obtained from looking at the graph.
From the maximum height values, I calculated the maximum potential energy per unit mass (U/m) of the ball in the middle of each interval. So for max height for the first interval I got: U = (9.8 m/s^2)(0.686 m) = 6.733 m2/s2 (U/m) for the second one I got 4.939 U/m and the third one I got 3.685 U/m.

My question is: determine the amount of mechanical energy (per unit mass) that the ball loses during the three selected impacts with the ground

Homework Equations

The Attempt at a Solution

I know that U/m (potential energy) is equal to E/m (mechanical energy) of the ball when it is in free flight but I'm not sure how to find the mechanical energy lost between bounces...do I just subtract the values and the difference is the loss?
Thanks in advance!

 

[TSny]

What does the height of .686 m represent? Is it the initial height of the ball when it was dropped or is the the max height after the first bounce?

For the mechanical energy lost during the first impact you will need to determine the mechanical energy just before impact as well as the energy just after impact.

 

[amanda.ka]

What does the height of .686 m represent? Is it the initial height of the ball when it was dropped or is the the max height after the first bounce?

For the mechanical energy lost during the first impact you will need to determine the mechanical energy just before impact as well as the energy just after impact.

It represents the max height after the first bounce and the other 2 subsequent values equal the max height of the 2nd and 3rd bounce. So mechanical energy before impact would all be all gravitational potential energy (U = gy) and energy just after the impact would be all kinetic (1/2mv^2) correct?

 

[TSny]

Just before impact, all of the mechanical energy is in the form of kinetic energy. And just after impact all the mechanical energy is again kinetic (but not the same amount as before impact).

How can you determine the kinetic energy just before impact? Think about where that kinetic energy came from.

 

[amanda.ka]

Just before impact, all of the mechanical energy is in the form of kinetic energy. And just after impact all the mechanical energy is again kinetic (but not the same amount as before impact).

How can you determine the kinetic energy just before impact? Think about where that kinetic energy came from.

The kinetic energy is being transformed from the potential energy. So as the ball is falling to the ground the potential energy decreases to 0 while the kinetic energy increases until it's all kinetic before the impact. Therefore, KE before impact would be equal to PE (in my case 6.733)?

 

[TSny]

Therefore, KE before impact would be equal to PE (in my case 6.733)?

This is not the correct value of PE to use to obtain the energy before the first impact. You said that the height of 0.686 m is the height to which the ball bounces after the first impact.

 

[insightful]

The kinetic energy is being transformed from the potential energy. So as the ball is falling to the ground the potential energy decreases to 0 while the kinetic energy increases until it's all kinetic before the impact. Therefore, KE before impact would be equal to PE (in my case 6.733)?

Yes. It would also be instructive to calculate the fraction (or percent) energy lost per bounce.

 

[amanda.ka]

This is not the correct value of PE to use to obtain the energy before the first impact. You said that the height of 0.686 m is the height to which the ball bounces after the first impact.

If the ball starts by being at initial height (H0) of 0.925 m, drops to the floor and bounces up to a smaller height (H) of 0.686 m then would loss of energy = mg(H0-H)? So before the first impact PE would be (9.8)(0.925) = 9.065? Also sorry for the delayed response, I had some computer troubles over the last few days.

 

[TSny]

If the ball starts by being at initial height (H0) of 0.925 m, drops to the floor and bounces up to a smaller height (H) of 0.686 m then would loss of energy = mg(H0-H)? So before the first impact PE would be (9.8)(0.925) = 9.065?

Yes, that's right.

Also sorry for the delayed response, I had some computer troubles over the last few days.

No problem.

 

[amanda.ka]

Yes, that's right.No problem.

awesome, thank you!