Calculating Speed, Angular Velocity, and Tension in Circular Motion of a Gymnast

[Scarlet_pat]

Homework Statement

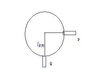
a gymnast of mass 75kg swinging from at a point p on a light rope to point Q. the circular arc through his centre of mass has radious of 10m

calculate:
speed at Q
angular velocity at Q
tension of string at point Q

Homework Equations

centripetal force
f=ma, f=m * v^2/r
omega (w) = v/r
maximun tension of vertical motion, F= T + mg ; T = F - mg

The Attempt at a Solution

Speed at Q

since F = ma = 75 x 9.8 =735 N
therefore the centripetal force of the circle is = 735 N

using F = m * v^2/ r
solve for v ... root F*R/m= V = root 735 x 10/75 = 9.9m/s

angular velocity:
since v =rw ; v/r =w 9.9/10 = 0.99 rad/s

tension at point Q
maximim tension is F= T=mg ; f-mg = T = 735 - 735 = 0 N

T shouldn't be 0 N...


i think i have made a mistake from the beginning, did i use the right equation to obtain centripetal force ?

 

[gneill]

With F = ma you've calculated the gymnast's weight, not the centripetal force at the bottom of the arc, which will depend upon his speed.

Can you think of a way to find the gymnast's kinetic energy at the bottom of the arc?

 

[Scarlet_pat]

With F = ma you've calculated the gymnast's weight, not the centripetal force at the bottom of the arc, which will depend upon his speed.

Can you think of a way to find the gymnast's kinetic energy at the bottom of the arc?

thank you for replying

check this out

F=ma ... while a - rw^2
F=mrw^2 ... while w =v/r
F= m* v^2 / r ...
and that is why i claimed that F =ma will gives me centripetal force


Time was not given in the question therefore other equation is a no-go
such as theta = s/ r or v= s /t

 

[gneill]

thank you for replying

check this out

F=ma ... while a - rw^2
F=mrw^2 ... while w =v/r
F= m* v^2 / r ...
and that is why i claimed that F =ma will gives me centripetal force

Well, unfortunately it is not the case, since his acceleration at the bottom of the arc is not just g, the acceleration due to gravity.

Time was not given in the question therefore other equation is a no-go
such as theta = s/ r or v= s /t

Have you considered conservation of energy?

 

[Scarlet_pat]

Well, unfortunately it is not the case, since his acceleration at the bottom of the arc is not just g, the acceleration due to gravity.



Have you considered conservation of energy?

well my teacher has never ever mention anything about conservation of energy while we are doing circular motion, therefore i doubt that.
however ... which formula should i use to obtain centripetal force then ?

 

[gneill]

The first thing you want to find is the speed of the gymnast at the bottom of the arc. What has supplied his kinetic energy?

 

[Scarlet_pat]

according to the diagram... he starts at point P to point Q... therefore... his mass and gravity would be the elements which supplied his kinetic energy .. i suppose ?

 

[gneill]

according to the diagram... he starts at point P to point Q... therefore... his mass and gravity would be the elements which supplied his kinetic energy .. i suppose ?

Yes, and specifically, the gravitational potential energy of his mass. If you can work out his change in gravitational potential energy, then you have his kinetic energy (since PE has been traded for KE as he falls).

 

[Scarlet_pat]

but then i don't not have the distance between the two objects ... in this case ... position. in the formula of gravitation acceleration requires distances =.=!

 

[gneill]

but then i don't not have the distance between the two objects ... in this case ... position. in the formula of gravitation acceleration requires distances =.=!

Surely you can determine the difference in height between points P and Q?

 

[Scarlet_pat]

height ..? i thought it'd be the distance of the arc... p - q

 

[gneill]

Height. Gravitational potential depends upon radial distance from the center of the Earth (in the large scale), and when working over small distances near the surface of the Earth it depends upon change in height.

 

[Scarlet_pat]

ok then... therefore ... what would be the distance in this case...:( sorry ...

and the formula is - GM/ r^2 * unit vector?

 

[gneill]

What's the radius of the circle he's swinging through? If he starts at the same height as the circle center, what's his change of height when he moves to the bottom of the circle?

For an object of mass M near the surface of the Earth,

ΔPE_{gravitational} = M*g*Δh

M is the mass of the body that's changing height. Δh is the change in height.

 

[Scarlet_pat]

omg... -.- i didnt know that it uses the same formula.. thank you thank you...
after i find the PE - gravitational...
based on the formula my teacher gave me, none of them has have corelation with Energy...

PE = KE , work = F x distance ( height perhaps ? )
F= work / Distance?

 

[gneill]

omg... -.- i didnt know that it uses the same formula.. thank you thank you...
after i find the PE - gravitational...
based on the formula my teacher gave me, none of them has have corelation with Energy...

PE = KE , work = F x distance ( height perhaps ? )
F= work / Distance?

In the case of the gravitational force doing work, distance = change in height, and f = M*g, the weight of the object. So, work = M*g*Δh.

That work done is going to end up as kinetic energy. How do you relate kinetic energy to speed?

 

[Scarlet_pat]

i do understand the work = mgh formula ..

E = Mv^2 right ?!

 

[gneill]

Half of that. KE = (1/2) M v²

 

[Scarlet_pat]

ok it makes perfect sense .. now ... thank you very much...:D
thank you thank you
thanks for your time

 

[gneill]

No problem. Glad to help. Good luck.