Calculating Tension and Acceleration in a Pulley System with Applied Force

[ehild]

Homework Statement

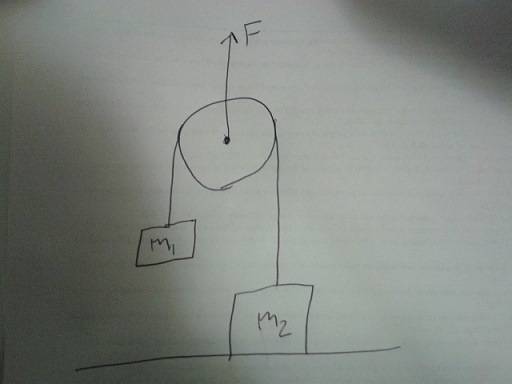
A force of 25 N is applied on the pulley. M1 = 1.5 kg, M2 = 2.5 kg, light frictionless strings and pulley.

a) What is the tension in the strings?
b) What is the acceleration of the masses?
c) What is the minimum Force to apply on the pulley so that M2 comes off the ground?

Homework Equations

ƩF = ma

The Attempt at a Solution

I am not totally sure how to do this question because of the extra force applied. I mean since there is another acceleration, I am thinking in my head that it won't be just mg but it will be something like m(g+ 25/9.8) but I am not sure. Also it seems like there won't be an acceleration in mass 2, but will be in mass 1. Can anyone point me in the right direction?

Yes, the pulley also accelerates. First you have to figure out the tension. The pulley is massless, so its mass times acceleration is zero: the net force acting on the pulley has to be zero. The net force is F-2T=0. Now you have T. What is it?

What forces act on the heavier mass? It is on the ground. There is an upward force T and the downward force _m2g. If it is negative (is it?) the block can not accelerate upward. But it can not move downward, because of the support. Its acceleration is zero. The net force includes also the normal force and the sum of all forces is zero. The block stays on the ground. . How much should be F so it can rise?

You know T, so it is easy to find the acceleration of m1 from the equation you have shown : m₁a₁=T-m₁g.

You see that the accelerations are not the same!

ehild

 

[Kishlay]

how did you put that image on the question??

 

[Panphobia]

URL not relevant to the question, but there it is.

 

[haruspex]

So F and T are in the same direction?

The direction of T depends on your standpoint. For the pulley, the Ts act downwards; for the masses, upwards.
Just to point out something I didn't notice mentioned elsewhere in the thread: the two tensions are the same because the pulley is massless (and frictionless). No mass means no moment of inertia, so no torque required to accelerate it on its axis.