Calculating Tensions and Acceleration in Frictionless Pulley System

[Lamoid]

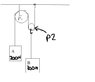
The weights of the objects are 200 N and 300 N. The pulleys are essentially frictionless and massless. P1 has a stationary axle but P2 is free to move up and down. Find the tensions FT1 and FT2 and the acceleration of each body.

Diagram I made in paint attached.

Now my problem is not that I can't get the right answer but that I don't understand why. It gives me a hint that the acceleration of block B is half (and in the opposite direction of course) that of block A and I cannot not figure out why that is. Can anyone explain it to me?

And yes, the diagram sucks but the A block is moving down, B is moving up.

 

[Doc Al]

You can prove mathematically that the magnitude of the acceleration of A is twice that of B using the fact that the string length remains constant. Divide the string into three pieces: X (from mass A to P1), Y (from P1 to P2), Y (from P2 to the spot of rope at the height of P1). Thus the length of the rope is X + 2Y. Since the length can't change, take the derivative twice to find the acceleration constraint: a_x + 2a_y = 0. Make sense? (a_x is the acceleration of mass A; a_y is the acceleration of mass B)

But even better than proving it is to just play around with a piece of string and see how folding the string in half affects things.

 

[Lamoid]

Thank you very much! That's a neat calculus proof.