Calculating the height after an elastic collision

[bna10]

Homework Statement

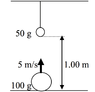
A ball of mass 100 g is projected straight up with a speed of 5 m/s from the floor. Another ball of mass 50 g is hung from the ceiling by a light string at a height of 1.00 m directly above the first ball, so that the projected ball collides elastically with it. Calculate the height above the floor to which the smaller ball will rise.

Homework Equations

1/2 M1V1i^2 = 1/2 M1V1f^2 + 1/2 M2V2f^2

The Attempt at a Solution

When I use the equation above it gives me two unknown variables V1f and V2f (after the collision). but I don't know what equation to use to figure out Δy.

 

[krome]

You're using conservation of energy. Energy is not the only thing conserved in elastic collisions. In fact, the thing I'm thinking of is conserved even in inelastic collisions.