Calculating the Length of a Segment Joining Centers of Inscribed Circles
- Thread starter Chikawakajones
- Start date
Click For Summary
SUMMARY
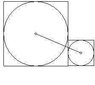
The discussion focuses on calculating the length of the segment joining the centers of inscribed circles of two squares with areas of 4 cm² and 196 cm². The correct method involves constructing a right-angled triangle where the hypotenuse is the segment connecting the centers. The accurate calculation yields a length of 10 cm, derived from the formula d = √(6² + 8²). Participants debated various methods, with Mahesh's approach being validated as correct, while others presented incorrect calculations.
PREREQUISITES- Understanding of basic geometry concepts, including inscribed circles and right-angled triangles.
- Familiarity with the Pythagorean theorem for calculating distances.
- Ability to calculate the area of squares and derive side lengths from area values.
- Knowledge of square roots and their application in geometric calculations.
- Study the properties of inscribed circles in polygons.
- Learn more about the Pythagorean theorem and its applications in geometry.
- Explore geometric constructions using compass and straightedge techniques.
- Practice solving problems involving distances between points in coordinate geometry.
Students, educators, and math enthusiasts seeking to enhance their understanding of geometry, particularly in relation to inscribed circles and triangle properties.
Similar threads
- · Replies 9 ·
- · Replies 59 ·
- · Replies 27 ·
- · Replies 15 ·
- · Replies 9 ·
- · Replies 14 ·
- · Replies 3 ·
- · Replies 22 ·
- · Replies 6 ·