maxim07
- 53
- 8
- Homework Statement
- If the three slits have equal widths, show that intensity I1 of light on the screen as a function of y is I = I/9[1 + 2cos(2pi * dy/Rw)]^2 where w is wavelength
If the width of the central slit is made twice as wide show that the intensity becomes I = 16I/9cos^4(pi*dy/Rw)
- Relevant Equations
- Sin/cosine addition formulas
Here’s an image of the equations better layed out

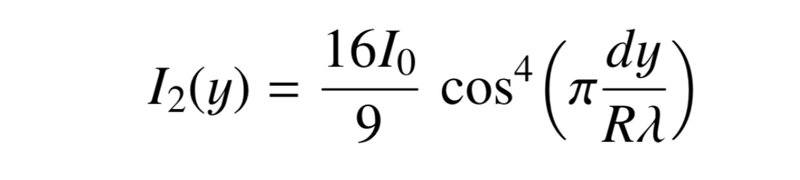
here’s the solution, I don’t understand how they are squaring it to get the time average

here’s the solution, I don’t understand how they are squaring it to get the time average