Calculating Triangle Area: S1, S2 and ABF

[Semo727]

Triangle Area

Hello!
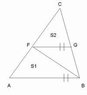
I came across this: On the picture there is triangle ABC with the unknown area S. All we know is, that area of triangle ABF is S1 and area of FGC is S2. And line AB is parallel with line FG. What is the area of triangle ABC? Thanks for your help!

Im sorry for title of this thread: Triangle volume, I wanted to say "area"(a^2).

And now, I will write what I managed to get:
S=\frac{S_2}{2}+S_1+\sqrt{\frac{S_2^2}{4}+S_1 S_2 }
but, I'm not sure if its right and I don't like the way I got it, could you please tell me what was your way?

 

[topsquark]

Hello!
I came across this: On the picture there is triangle ABC with the unknown area S. All we know is, that area of triangle ABF is S1 and area of FGC is S2. And line AB is parallel with line FG. What is the area of triangle ABC? Thanks for your help!

Im sorry for title of this thread: Triangle volume, I wanted to say "area"(a^2).

And now, I will write what I managed to get:
S=\frac{S_2}{2}+S_1+\sqrt{\frac{S_2^2}{4}+S_1 S_2 }
but, I'm not sure if its right and I don't like the way I got it, could you please tell me what was your way?

I don't know how you got it, but my answer is the same, so at least you know it's correct.

-Dan