Calculating Velocity of Water Flow in Open Channel

[Kqwert]

Homework Statement

[/B]
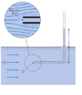
We have water flowing in an open channel. A small tube is placed in the channel, and the water raises to a height "l" above the water surface. The distance from the water surface to point 1/2 (points are at same height) is d. At point 1 the fluid velocity is V1 and at point 2 it is zero (stagnation point). Calculate the water velocity V1. (Figure below for help)

Homework Equations

Bernoulli:
(1/2)*V^2 + P/rho + g*z = constant.

The Attempt at a Solution

First I calculate the stagnation pressure Ps, by using Bernoulli from 1 to 2. This yields:

(1/2)*V1^2 + P1/rho = 0 + P2/rho

Ps = rho*(1/2)*V1^2 + P1

Then I calculate the pressure through the tube, where we have hydrostatic conditions. P0 is the atmospheric pressure.:

Ps = P0 + rho*g*l + rho*g*d.

My question is:

under which conditions can we assume that P1 = rho*g*d, i.e. under which conditions can we assume that the pressure at point 1 is independent of the fluid flow at that point? Is it only when the fluid flow is ONLY horizontal?

 

[rude man]

under which conditions can we assume that P1 = rho*g*d, i.e. under which conditions can we assume that the pressure at point 1 is independent of the fluid flow at that point? Is it only when the fluid flow is ONLY horizontal?

It's an open channel. Think of standing by a river moving at any speed. What would you expect the pressure to be at a depth d?

 

[Kqwert]

It's an open channel. Think of standing by a river moving at any speed. What would you expect the pressure to be at a depth d?

If it´s moving I would assume that it would be dependent on the depth d but also the speed the river is moving

 

[Chestermiller]

If it´s moving I would assume that it would be dependent on the depth d but also the speed the river is moving

Since the flow is horizontal, as we said in the other thread, the pressure variation is hydrostatic in the vertical direction (at least in a region undisturbed by the pitot tube).

 

[rude man]

If it´s moving I would assume that it would be dependent on the depth d but also the speed the river is moving

Can you have a sudden change in pressure as you go from just above its surface to just below? So what must presure be just below? And so the pressure at a depth d?

 

[Dr Dr news]

Measurement of fluid velocity with a Pitot tube is based on Bernoulli's equation which represents the conservation of energy per unit volume of fluid flow. p(total), pt, represents the total energy; p(static), ps, represents the potential energy: and q = ρU^2 / 2 = dynamic pressure, represents the kinetic energy. So pt - ps = q, solving for U =√2(pt - ps)/ρ. With your probe you are measuring pt so you need to calculate ps based on the hydrostatic pressure at depth d. And do not forget to account for the atmospheric on top of the open channel and the open top of your probe.

 

[Kqwert]

Since the flow is horizontal, as we said in the other thread, the pressure variation is hydrostatic in the vertical direction (at least in a region undisturbed by the pitot tube).

Thank you, but what would happen if we also had a flow component in the z-direction?

 

[Kqwert]

Can you have a sudden change in pressure as you go from just above its surface to just below? So what must presure be just below? And so the pressure at a depth d?

I am not exactly sure what you are trying to say?

 

[Chestermiller]

Thank you, but what would happen if we also had a flow component in the z-direction?

It depends on (a) if the fluid velocity is accelerating in the z direction and (b) if the fluid were being regarded as inviscid or viscous.

 

[rude man]

I am not exactly sure what you are trying to say?

I am trying to show that the pressure just below the surface is the same as above, i.e. atmospheric, regardless of the flow velocity.
OK, we have a river, not flowing. A block of wood floats on it, half-in, half-out. Now the river starts to flow. Is the block still submerged 50-50?

 

[Chestermiller]

I am trying to show that the pressure just below the surface is the same as above, i.e. atmospheric, regardless of the flow velocity.
OK, we have a river, not flowing. A block of wood floats on it, half-in, half-out. Now the river starts to flow. Is the block still submerged 50-50?

Irrespective of the flow, if surface tension effects are negligible and the fluid is inviscid, pressure is continuous across a phase boundary. For a viscous fluid, the traction vector(which includes the pressure) is continuous.

If you carry out a force balance on a differential element of surface area within the interface (which has no mass), the forces exerted by the fluids situated on the two sides of the interface must match (since ma = 0).

 

[Dr Dr news]

This is not that complicated. The total pressure in the Pitot tube is q + p(static) and p(static) = ρgh + p(atmospheric). The conversion factor is 406 inches water = 1 atmosphere = 101.3 kPa. U(m/s) = √2q(n/m^2) / ρ(kg/m^3) The sensitivity of the Pitot tube to crossflow is of course dependent on the relative magnitude of the crossflow. I found in an experiment measuring the airspeed of an automobile, that a crosswind of 10 mph gusting to 15 mph had an effect on the measurement of the ground speed at 20, 30. and 40 mph of less than 10%.