Calculating Voltages Across Resistors Using Ohm's Law

[Rugile]

Homework Statement

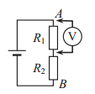
Two resistors are connected in series to an ideal battery. When the voltmeter is connected in parallel to one of the resistors, it showed 6V; when connected in parallel to another resistor it showed 4V. When the voltmeter was connected in parallel to both resistors (connected to pins A and B, see attachment) it showed 12V. What were the voltages across both resistors before the voltmeter was connected?

Homework Equations

Ohm's law

The Attempt at a Solution

I guess we can say from the third measurement that the voltage of the supply is 12V. Now the voltage across the first resistor is normally $V_1 = V * \frac{R_1}{R_1 + R_2}$, where V is the supply voltage. Although when the voltmeter is connected due to its internal resistance the voltage across 1st resistor changes; then the voltage across the voltmeter and the first resistor is $V_1' = V * \frac{R_{01}}{R_{01}+R2}$, and $R_{01} = \frac{R_1 * r}{R_1 + r}$, r is the voltmeter resistance. Thus $V_1' = V * \frac{R_1r}{R_1r + R_2R_1 + R_2r}$. Same calculations can be made for the second resistor. Is that right? I can't figure out what to do next - any help appreciated.

 

[BvU]

So you have expressions for $V_1'$ and for $V_2'$. You know the ratio is 4/6. What does that say about $R_1/R_2$ ?

 

[ehild]

The Attempt at a Solution

I guess we can say from the third measurement that the voltage of the supply is 12V. Now the voltage across the first resistor is normally $V_1 = V * \frac{R_1}{R_1 + R_2}$,

The question is what would be the voltages without the voltmeter. You wrote the expression for V1, you can write it in terms of R2/R1. On the same way, you can find V2 in terms of R1/R2.

R1/R2 can be found from the ratio of the measured voltages, as BvU suggested.

ehild

 

[Rugile]

Yes, thank you very much! Was quite close to the answer myself, I guess :)

 

[ehild]

Yes, you were quite close, needed just a little push

ehild