Calculating work done in this thermodynamic cycle

[Urmi Roy]

Homework Statement

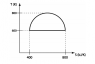
In the thermodynamic cycle as shown,
a) What is the direction that the cycle is executed-clockwise or anticlockwise?
b) What is the work done?

Homework Equations

First law of thermodynamics for a cycle

E2-E1= Q-W= Tds-Pdv=0

The Attempt at a Solution

a) I know that it should be clockwise because I read that when ∫Tds is positive, the cycle on a T-S diagram should be represented in the positive direction. However, I don't understand this completely.

b) I know it is the area inside the semicircle, but I don't know how I'm going to integrate it.

 

[Chestermiller]

First law of thermodynamics for a cycle

E2-E1= Q-W= Tds-Pdv=0

Hi Urmi. How's it going?
Your first law equation above is incorrect. It should read:

E2-E1= Q-W= ∫Tds-∫Pdv=0. Note the integral signs.

As a result of this, because the change in internal energy around the cycle is zero, you must have that:

∫Pdv=∫Tds

What is the equation for the amount of work done in this reversible process on the surroundings?

Chet

 

[Urmi Roy]

Hi Chet! I'm doing fine. Preparing for H&M transfer next sem and revising thermo a bit.

So I understand about the integrals. As to your question, isn't it just that the area under the T-dS plot? Since we don't know what type of processes are represented by each line (adiabatic/polytropic) except for the straight line part (which is isothermal) we don't really have a formula to calculate the work, right?

 

[Chestermiller]

Hi Chet! I'm doing fine. Preparing for H&M transfer next sem and revising thermo a bit.

So I understand about the integrals. As to your question, isn't it just that the area under the T-dS plot? Since we don't know what type of processes are represented by each line (adiabatic/polytropic) except for the straight line part (which is isothermal) we don't really have a formula to calculate the work, right?

Once you assume that the cycle is reversible, you have what you need. In that case P is the pressure of the gas, and the area of the cycle on the TS plot is equal to the work. You are not calculating the work directly from PdV, but you are using what you know about the first and second laws to deduce the amount of work.

Chet

 

[Urmi Roy]

Yup, that's what I said in the first post too. However, (maybe this is a math question) How do I calculate the area here? Its not just π*r^2...

Also you didn't say anything about the clockwise/anti clockwise concept...

 

[Chestermiller]

Yup, that's what I said in the first post too. However, (maybe this is a math question) How do I calculate the area here? Its not just π*r^2...

Also you didn't say anything about the clockwise/anti clockwise concept...

Actually, if you look at the scales on S and T, to the eye it looks like, coincidentally, the integral actually is πr²/2. Regarding clockwise or anticlockwise, it depends on whether the system is doing work on the surroundings or whether the surroundings are doing work on the system. The problem doesn't say.

 

[Urmi Roy]

Right, so since the radius is 200K (along the temperature axis) and 200 KJ/K for the entropy axis, it's just pi*(200)^2?

Referring to (http://en.wikipedia.org/wiki/Thermodynamic_cycle), I'm guessing even though in a cycle the net work is the same whether you go clockwise or anticlockwise, if you go anticlockwise, you're subtracting a larger value from the smaller value...so its negative...similarly in a T-S diagram.

I hope this sounds good.

 

[Chestermiller]

Right, so since the radius is 200K (along the temperature axis) and 200 KJ/K for the entropy axis, it's just pi*(200)^2?

It's a semicircle, not a circle.

Referring to (http://en.wikipedia.org/wiki/Thermodynamic_cycle), I'm guessing even though in a cycle the net work is the same whether you go clockwise or anticlockwise, if you go anticlockwise, you're subtracting a larger value from the smaller value...so its negative...similarly in a T-S diagram.

I hope this sounds good.

Just figure out which direction makes the integral of TdS positive and which direction makes it negative (on your figure).