Calculations for accelerating particles in a Cyclotron

In summary, calculations for accelerating particles in a cyclotron involve determining the radius, frequency, and magnetic field strength necessary to achieve the desired energy levels. The cyclotron uses a uniform magnetic field to bend the path of charged particles into a spiral, allowing them to gain energy with each revolution. Key equations include the relationship between the particle's velocity, the magnetic field, and the radius of the circular path, as well as the cyclotron frequency, which is dependent on the charge-to-mass ratio of the particles. These calculations ensure efficient acceleration and optimal performance of the cyclotron in various applications, such as nuclear physics and medical therapies.
  • #1
sss1
50
2
Homework Statement
Picture
Relevant Equations
mv^2/2, f=qB/2pim
For this question part d, KE=mv^2/2=q^2B^2r^2/2m (I rearranged B=mv/qr for v and subbed into mv^2/2). q^2b^2r^2/2m=2F_cyc^2r^2m(pi)^2
But when I subbed the values in I got 16.45MeV but the answer says 165keV instead. I'm not sure what went wrong?

What's a good explanation for part e also?
1699426550694.png
1699426556922.png
 
Physics news on Phys.org
  • #2
sss1 said:
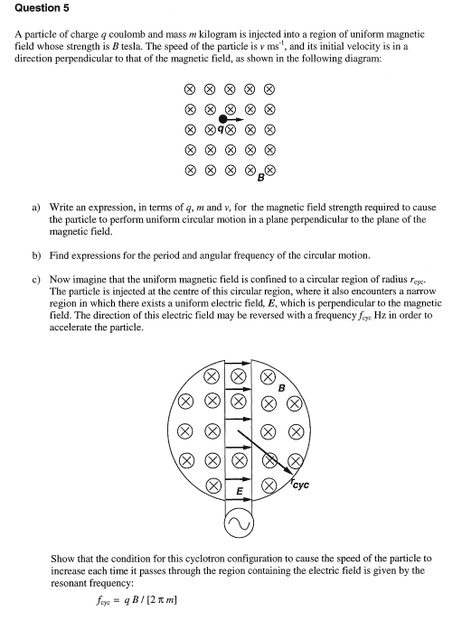
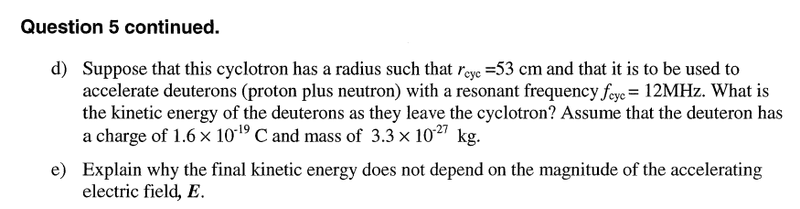
But when I subbed the values in I got 16.45MeV but the answer says 165keV instead. I'm not sure what went wrong?
I got the same answer as you. (Except I rounded mine to an appropriate number of significant figures!)

It looks like the official answer is wrong - probably because whoever did it used r =53mm instead of r=53cm.

sss1 said:
What's a good explanation for part e also?
As you probably know, ther rules here require you to show your own thoughts/attempt before guidance is offered.
 
Last edited:
  • Like
Likes MatinSAR and berkeman
  • #3
Steve4Physics said:
As you probably know, ther rules here require you to show your own thoughts/attempt before guidance is offered
Well if the e field is strong, it’ll only take a few cycles until the particle leaves? Whereas if if the e field is weak, it’ll take a long time to leave the cyclotron, so the KE is the same regardless?
 
  • #4
sss1 said:
Well if the e field is strong, it’ll only take a few cycles until the particle leaves? Whereas if if the e field is weak, it’ll take a long time to leave the cyclotron, so the KE is the same regardless?
You need to do better than that. What is an expression for the kinetic energy of the particle just before it exits? Is there an ##E## in it?
 
  • Like
Likes MatinSAR, Steve4Physics and berkeman

FAQ: Calculations for accelerating particles in a Cyclotron

How does a cyclotron accelerate particles?

A cyclotron accelerates particles using a combination of a static magnetic field and a rapidly alternating electric field. The magnetic field forces the charged particles into a circular or spiral path, while the electric field, applied via electrodes called "dees," accelerates the particles each time they cross the gap between the dees.

What is the formula for calculating the kinetic energy of particles in a cyclotron?

The kinetic energy (K.E.) of particles in a cyclotron can be calculated using the formula: \( K.E. = \frac{1}{2} mv^2 \), where \( m \) is the mass of the particle and \( v \) is the velocity. Alternatively, for a particle with charge \( q \) and radius \( r \) in a magnetic field \( B \), the kinetic energy can also be given by \( K.E. = \frac{q^2 B^2 r^2}{2m} \).

How do you calculate the frequency of the alternating electric field in a cyclotron?

The frequency of the alternating electric field, also known as the cyclotron frequency, is calculated using the formula: \( f = \frac{qB}{2\pi m} \), where \( q \) is the charge of the particle, \( B \) is the magnetic field strength, and \( m \) is the mass of the particle.

What factors limit the maximum energy achievable in a cyclotron?

The maximum energy achievable in a cyclotron is limited by several factors, including the strength of the magnetic field, the size of the cyclotron, the relativistic effects at high velocities, and the ability to maintain synchronization of the alternating electric field with the particle's motion.

How do relativistic effects impact particle acceleration in a cyclotron?

As particles approach relativistic speeds (close to the speed of light), their mass effectively increases due to relativistic effects. This causes the cyclotron frequency to decrease, leading to a loss of synchronization between the particles and the alternating electric field. This limits the maximum velocity and energy that can be achieved in a traditional cyclotron.

Similar threads

Solving Orbital Speed with Energy & Angular Momentum Conservation
Replies
7
Views
2K
Cyclotron magnetic field questions
Replies
4
Views
12K
Using energy considerations to analyse particle motion
Replies
3
Views
575
What is the estimated path length traveled by a deuteron in a cyclotron?
Replies
4
Views
3K
Electric Potential inside an insulating sphere
Replies
11
Views
4K
Finding a Parametric Solution for Particle Trajectory in Magnetic Field
Replies
3
Views
1K
Uniform circular motion for proton and 2 particles
Replies
2
Views
992
Solve Cyclotron Question: Calculate Magnetic Field & Time to Exit
Replies
6
Views
6K
Charged particle moving in circular path in a magnetic field
Replies
7
Views
1K
Circular trajectory traveled by a charged particle in a magnetic field
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top