MHB Calculus: Maximum point for revenue function

[Doffy]

Hello (Smile). I have been stuck on this question for a while.

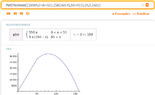
A company charges $550 for a transistor set on orders of 50 or less sets. The charge is reduced by $5 per set for each order in excess of 50 sets. Find the largest size order company should allow so as to receive a maximum revenue.

I have tried to formulate the revenue function as: R(x) = (550 -5x) x, for x > 50.
Am I right? The answer mentioned in book is 80 sets.

 

[MarkFL]

Your revenue function isn't right...we are only subtracting \$5 per set in excess of 50 ordered, hence:

$$R(x)=x(550-(x-50)5)$$

So, simplify and factor, and then you know that the vertex will lie on the axis of symmetry which will be midway between the two roots.

 

[Doffy]

Ok, I understand now. Thanks for helping.

 

[MarkFL]

Ok, I understand now. Thanks for helping.

What we should actually write for the revenue function is a piecewise defined function:

$$R(n)=\begin{cases}550n, & 0<n<51 \\[3pt] 5n(160-n), & 50<n \\ \end{cases}$$

I used $n$ rather than $x$ to indicate that the independent variable is discrete rather than continuous. Then we may plot this function:

View attachment 5104

We see that the linear portion of the function increases at a constant rate (given by the slope of the line), and then we should observe that the parabolic portion of the function opens downward (since the coefficient of the squared term is negative) and so its maximum will be at the vertex, which lies on the axis of symmetry, which will be midway between the roots, at $n=0$ and $n=160$, which is:

$$n=\frac{0+160}{2}=80$$

Since this value is to the right of where the linear and parabolic portions "meet," we may conclude:

$$R_{\max}=R(80)$$