Calculus Questions with Vectors (cross product)

[advityakhanna]

Homework Statement

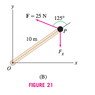
Calculate the net torque about O at P,assuming that a 30-kg mass is attached at P [Figure 21(B)]. The force Fg due to gravity on a mass m has magnitude 9.8m m/s2 in the downward direction.

Homework Equations

The torque about the origin O due to a force F act- ing on an object with position vector r is the vector quantity τ = r × F. If several forces Fj act at positions rj , then the net torque (units: N-m or lb-ft) is the summation of r cross product F.

The Attempt at a Solution

Have solution for no mass hanging that is: r=OP =10(cosθi+sinθj) The angle between the force vector F and the x-axis is (θ + 125◦), hence, F = 25 (cos (θ + 125◦) i + sin (θ + 125) j)
The torque τ about O acting at the point P is the cross product τ = r × F. We compute it using the cross products of the
unit vectors i and j:
τ =r×F=10(cosθi+sinθj)×25((cosθ+125◦)i+sin(θ+125◦))j = 250 (cos θ i + sin θ j) × ((cos θ + 125◦) i + (sin θ + 125◦) j)= 250 (cos θ sin (θ + 125◦) k + sin θ cos (θ + 125◦) (−k))
= 250(sin(θ +125◦)cosθ −sinθ cos(θ +125◦))k
We now use the identity sin α cos β − sin β cos α = sin(α − β) to obtain
τ = 250sin(θ +125◦ −θ)k = 250sin125◦k ≈ 204.79k

 

[SteamKing]

It's really hard to follow your calculations because you have a LOT of these question mark thingies in the OP.

 

[Jufro]

The method looks good but wouldn't you want the force to be:

25 (cos (θ + 125◦) i + sin (θ + 125) j)- (30*g) j

The added term would account for the mass trying to rotate the arm itself.

Or is the 25 N force the net force on the mass (I thought it was an external force in addition to that of gravity)?