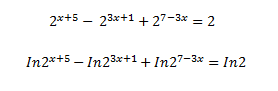The most common way of solving a problem like this in an elementary fashion is to try to get it into the form of a polynomial equation that can be easily solved. Of course, the question has to be set specifically so that it's "easy" to solve that way, and in this case, it is.
You need to be familiar with the rules of exponentiation. These are what you need: ##a^{b+c} = a^b \cdot a^c## and ##a^{bc} = (a^b)^c##
Using those rules, you can convert your equation into a sextic (power-6) equation in terms of a new variable ##y##, where ##y = 2^x##. This equation (thankfully) has at least one nice integer solution, which you can quickly find by trial and error (aided by the Rational Root Theorem,
http://www.purplemath.com/modules/rtnlroot.htm).
At this point you need to find the full solution set, or at least show there are no other real, positive solutions (since an exponential is strictly positive). You can do this by either polynomial long division or the much simpler synthetic division (
http://www.purplemath.com/modules/synthdiv.htm) by the linear factor you uncovered in the last step to get a quintic (power-5) polynomial. It's "tough" to solve or even sketch this curve, but fortunately, there is a little trick called the Decartes' Rule of Signs (
http://www.purplemath.com/modules/drofsign.htm) that allows you to very quickly conclude that the quintic has no positive real roots. Hence the single value for ##y## you've already found is the only one that is valid.
Finally, you find ##x## by solving ##2^x = y## for ##x##, which I assume you know to do. In the general case you can do so by taking logs of both sides, but here all that's required is simple inspection (this should give you a big hint about how "nice" the solution is).
(Edited for more details, since I was rushing to work in the morning and was unable to complete the post).