SUMMARY
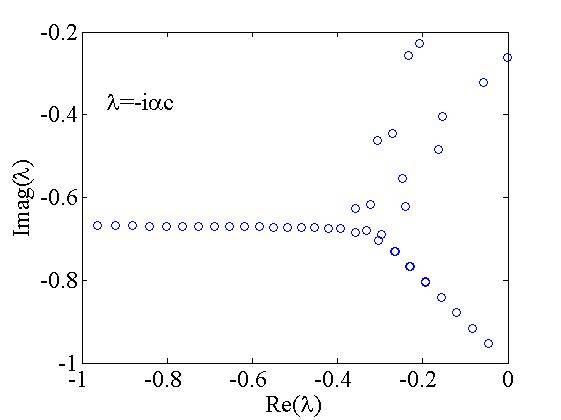
The discussion focuses on the interpretation of a plot related to the Orr-Sommerfeld equation, which is crucial for analyzing the stability of fluid flows. The plot represents the eigenvalue spectrum, where the imaginary part of the eigenvalue (Im(λ)) indicates frequency and the real part (Re(λ)) denotes growth rate. It is established that if Re(λ) is greater than zero, the corresponding eigenvalue signifies instability in the flow. The confusion arises from the orientation of the axes in the plot, which deviates from the typical representation.
PREREQUISITES
- Understanding of the Orr-Sommerfeld equation
- Familiarity with eigenvalue analysis in fluid dynamics
- Knowledge of complex numbers and their application in stability analysis
- Basic principles of fluid mechanics
NEXT STEPS
- Research the mathematical formulation of the Orr-Sommerfeld equation
- Study eigenvalue stability criteria in fluid dynamics
- Learn about the implications of complex eigenvalues in flow stability
- Examine different representations of eigenvalue spectra in stability analysis
USEFUL FOR
Fluid dynamics researchers, engineers analyzing flow stability, and students studying advanced fluid mechanics concepts.