SUMMARY
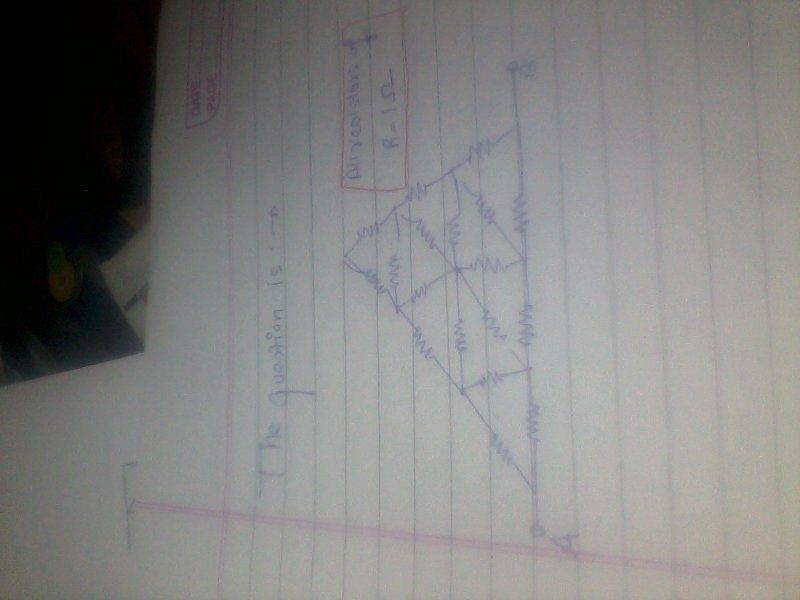
The discussion focuses on simplifying a resistor network using symmetry and Delta-Y transforms. Participants emphasize that by recognizing nodes at the same potential, one can simplify the circuit by connecting them or removing components without affecting circuit behavior. The primary method involves applying symmetry to identify parallel resistance opportunities and performing series/parallel resistor simplifications. Ultimately, the problem can be resolved with minimal Delta-Y transformations after applying symmetry techniques.
PREREQUISITES
- Understanding of resistor networks and circuit analysis
- Familiarity with Delta-Y (Δ-Y) transforms
- Knowledge of series and parallel resistor combinations
- Concept of electrical potential and node analysis
NEXT STEPS
- Study the principles of symmetry in electrical circuits
- Learn about Delta-Y (Δ-Y) transforms in depth
- Practice simplifying complex resistor networks using series and parallel combinations
- Explore advanced circuit analysis techniques, including Thevenin and Norton theorems
USEFUL FOR
Electrical engineers, circuit designers, and students studying circuit analysis who seek to enhance their understanding of resistor network simplification techniques.