Can the work of a counterclockwise cycle be positive?

[Soren4]

Consider an ideal gas following a thermodynamics cycle, represented on a $P-V$ plane. I read that if the cycle is "travelled" clockwise then $W_{gas, cycle}>0$ so the gas does positive work, while if the cycle is "travelled" counterclockwise then $W_{gas, cycle}<0$ but it seems to me that this cannot be always true.
For example take the cycle in the picture, made of two adiabatics and one isochoric.

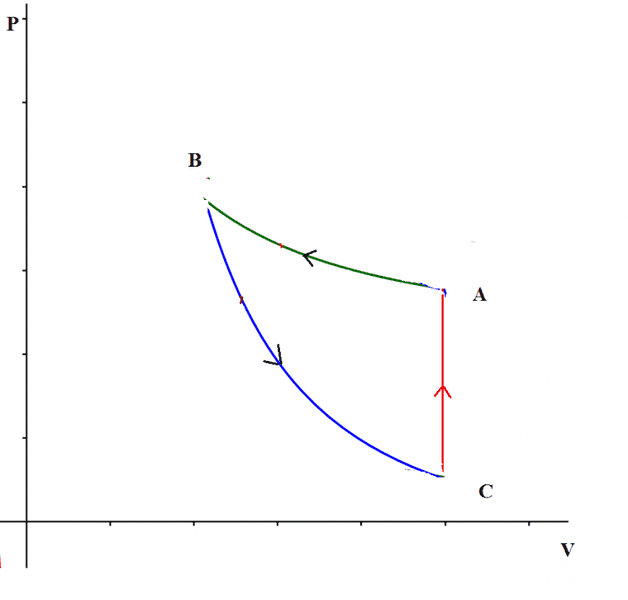
$$W_{cycle}=Q_{C->A}>0$$

So the work is positive even if the cycle is traveled anticlockwise.

So is the orientation of the cycle really a general rule to understand if work is positive or negative?

 

[Tazerfish]

The gas does negative work.

The work done in a gas can be defined as $\int P dV$
So the work is the surface under the p V curve.
The work done by the gas from B to C is shaded red. The gas does work since it expands.
The work done on the gas from the outside is the area that is striped blue. It is performed during the compression from A to B.
The blues striped area is bigger than the red shaded one so it takes more work to compress it than the work done by the gas during expansion.
The difference in work during both processes is shaded in green.
The statemen about "clockwise and anticlockwise" determining the sign of this work seems to be correct, not false as you implied.

 

[Soren4]

The gas does negative work.
View attachment 103015
The work done in a gas can be defined as $\int P dV$
So the work is the surface under the p V curve.
The work done by the gas from B to C is shaded red. The gas does work since it expands.
The work done on the gas from the outside is the area that is striped blue. It is performed during the compression from A to B.
The blues striped area is bigger than the red shaded one so it takes more work to compress it than the work done by the gas during expansion.
The difference in work during both processes is shaded in green.
The statemen about "clockwise and anticlockwise" determining the sign of this work seems to be correct, not false as you implied.

Thanks for the reply! But this is in constrast with the fact that, in any cycle, since $\Delta U=0$ we have $Q=W$, and in this case $Q$ is only the heat in the isochoric process, which is positive and this leads to $W>0$ necessarily.

 

[Tazerfish]

Thanks for the reply! But this is in constrast with the fact that, in any cycle, since $\Delta U=0$ we have $Q=W$, and in this case $Q$ is only the heat in the isochoric process, which is positive and this leads to $W>0$ necessarily.

Sorry to tell you this but no, Q is not only the heat in the isochoric process.
How can you follow an isothermal during compression ?
Without heat-flow, you would certainly follow an adiabatic curve not an isothermal.
The work you do during the compression of the gas in an isothermal is flowing to the outside as heat that leaves the system.
So we can conclude that you actually have more heat flow out of the system during the isothermal compression than the heat that is added during the isochoric heating.
If the only heat flow would happen during the isochoric heating then the diagram would not connect, it wouldn't be a cycle.
(And you would have positive work and heat flow.)

 

[Soren4]

Sorry to tell you this but no, Q is not only the heat in the isochoric process.
How can you follow an isothermal during compression ?
Without heat-flow, you would certainly follow an adiabatic curve not an isothermal.
The work you do during the compression of the gas in an isothermal is flowing to the outside as heat that leaves the system.
So we can conclude that you actually have more heat flow out of the system during the isothermal compression than the heat that is added during the isochoric heating.
If the only heat flow would happen during the isochoric heating then the diagram would not connect, it wouldn't be a cycle.
(And you would have positive work and heat flow.)

Thanks for the reply! I made a stupid example. If I got your point the cycle with A->B isochoric, B->C adiabatic and C->A adiabatic cannot exist. I looked for the reason of this and effectly in the case I proposed $\Delta S_{universe}=\Delta S_{environment}=\Delta S_{environment, A->B}<0$ which of course cannot be true. Is this the reason why B->C cannot be adiabatic too?

So I find another (hopefully possible) example of what I meant (or better the viceversa), in the following diagram.

One of the adiabatics must be irreversible otherwise the two curves cannot be connected (and it is improper to represent the irreverseible process on the diagram but I made it to make things clear). And also this (irreversible) cycle seems possible to me, since $\Delta S_{universe}=\Delta S_{environment}=\Delta S_{environment, A->B}>0$.

This cycle is clockwise, but $$Q_{cycle}=W_{cycle}=Q_{A->B}<0$$

Is this possible?

 

[Tazerfish]

There is something VERY wrong here.
I don't really know what it is... I suspect it is the irreversible adiabatic...
The way you drew it, the cycle would have a positive heat flow out(Isothermal compression) AND positive work.
Well, it isn't like conservation of energy is one of the most fundamental things EVER.

My best guess is that the blue line in your diagram is the pressure on the inside of the container somewhere.
The statement $\int p dV = W$ may not be correct anymore when you draw the diagram for an irreversible process(with p as a pressure somewhere in the container). You would need to consider the pressure at the piston surface, the pressure that you actually push against.
When considering the pressure at the interface, (since $\int p dV = W$ would work again if we did that) I suspect you would get a curve with two jumps.
So the curve actually "cuts" itself. And there is negative work done by the system.
It turns out I am horrible at drawing this but here's a try:

The rule would still work for the two individual surfaces.
EDIT: You are really going to great lengths just to break this rule
May I ask why ?

 

[Soren4]

There is something VERY wrong here.
I don't really know what it is... I suspect it is the irreversible adiabatic...
The way you drew it, the cycle would have a positive heat flow out(Isothermal compression) AND positive work.
Well, it isn't like conservation of energy is one of the most fundamental things EVER.

My best guess is that the blue line in your diagram is the pressure on the inside of the container somewhere.
The statement $\int p dV = W$ may not be correct anymore when you draw the diagram for an irreversible process(with p as a pressure somewhere in the container). You would need to consider the pressure at the piston surface, the pressure that you actually push against.
When considering the pressure at the interface, (since $\int p dV = W$ would work again if we did that) I suspect you would get a curve with two jumps.
So the curve actually "cuts" itself. And there is negative work done by the system.
It turns out I am horrible at drawing this but here's a try:View attachment 103052
The rule would still work for the two individual surfaces.
EDIT: You are really going to great lengths just to break this rule
May I ask why ?

Thanks a lot for the answer!

Don't want to find an exception to the rule! But I found these two cycles in two exercises and I wondered how to behave in this case. My only worry is (and I suppose the answer is yes):

In any "clockwise" cycle is the work done by gas positve? (And viceversa for "anticlockwise")?

In this way, when I look to a clockwise cycle I can surely say: "the work is positive"

 

[Tazerfish]

In any "clockwise" cycle is the work done by gas positve? (And viceversa for "anticlockwise")?

Yes. At least for reversible cycles that rule seems to be quite water-proof.
I already hinted at the mess irreversible cycles can cause (because the pressue in the diagram is not necessarily the pressure at the piston doing the work), so keep an eye out for that.

One last thing:
I usually find it more useful to remember a few very fundimental rules from which you can derive the others, rather than having a lot of specific rules.
For example, if you know that the work is $\int F(s) ds$ and know this :$p=\frac{F}{A}$
You can easily conclude that $\int p(V) dV$ is the work done in the compression or expansion of a gas.
From that you can derive that the are under the p-V curve is the work.
Clockwise means that the upper part of the cycle is an expansion(up moves right(more V)) and the lower part is a compression(down moves left(less V)).
That means that there is more work done during expansion than you do during compresssion.
With this thought you can basically proove the rule.
These things are so simple you are unlikely to forget them later on, and with that knowledge of the simple rules you can check or proove the more specific rules yourself. (Although the process does involve a little more thinking)
I hope this approach may help in the future.