Can You Solve These Vector Questions About Wind?

[uniquegirl]

Homework Statement

1 a) A kite skier is moving at 25 m s^1 in the N 25^0 E
direction as shown in the diagram. Calculate the
northerly and easterly velocity of the skier.

b) A strong gust of wind from the west causes the skier to accelerate to the east at 2.0 m s-2 for 1.8 s.
Calculate the new velocity in the easterly direction

c) Use your answer in (b) to calculate the size and direction of the new resultant velocity of the skier

Relevant Equations

N/A

N/A

 

[Lnewqban]

Start by drawing some vectors based on the description of the problem.

 

[kuruman]

According to our guidelines in order to receive help, you must show some effort towards the solution. Tell us what you think. "No idea where to start" is not showing an effort. It would also help if you figured out what equations are relevant and put them under heading "Relevant equations" where you actually put the statement of the problem. We provide the template to organize you and get you started so please, for future reference, use it appropriately.

 

[uniquegirl]

So a vector diagram, One arrow to the north, one somewhere in between North and east and one towards east.

 

[uniquegirl]

Would I use 25degrees sin/cos to find the northerly and easterly velocity?

 

[phinds]

DRAW A DIAGRAM. Then we can discuss it. If you have mistakes, we'll help you see where.

Also, "please help" is not really a helpful subject line.

 

[Steve4Physics]

For part 1a) you are being asked to find the northerly and easterly components of the given velocity vector.

If you truly have ‘no idea where to start’, watch the video below. It explains how to find the components of any vector, including the trigonometry you need. (Alternative videos can easily be found.)

You need to take the initiative; e.g.
- watch and understand the video;
- try solving part 1a) using what you have learned;
- post your working/answer here to get feedback.

Then 1b) and 1c) can be tackled.

 

[uniquegirl]

Thank you so much I really appreciate the help, I will figure out question 1 and then post the answers

 

[berkeman]

Thread closed for Moderation...

 

[fresh_42]

OP has been warned to show some efforts. I also changed the thread title: "Please Help!" is not a good idea.

As the OP promised to show us their solution of question 1, I will re-open the thread.

 

[uniquegirl]

My vector diagram is-

Attempt at 1a) Northerly velocity: Sin 25degrees=Vn/25
Vn= 25sin25degrees
= 10.56 ms^1 N
Easertly Velocity: Cos 25 degrees= vn/25
Vn= 25cos25 degrees
vn= 22.65 ms^1 E

 

[Lnewqban]

It seems that the location of West is not correct.

 

[TSny]

Attempt at 1a) Northerly velocity: Sin 25degrees=Vn/25

This is not correct.

$\sin 25^o$ and $\cos 25^o$ can be defined in terms of a right triangle where one of the angles in the triangle is $25^o$. "Side opposite", "side adjacent", and "hypotenuse" are involved.

Were you thinking in terms of a particular right triangle? If so, can you sketch or describe the triangle that you had in mind?

 

[uniquegirl]

It seems that the location of West is not correct.

sorry, I accidentally labelled it wrong in my diagram, I meant East

 

[Lnewqban]

Please, see:
https://www.physicsclassroom.com/class/vectors/Lesson-1/Vectors-and-Direction

Could you show us the “as shown in the diagram”.

 

[uniquegirl]

This is not correct.

$\sin 25^o$ and $\cos 25^o$ can be defined in terms of a right triangle where one of the angles in the triangle is $25^o$. "Side opposite", "side adjacent", and "hypotenuse" are involved.

Were you thinking in terms of a particular right triangle? If so, can you sketch or describe the triangle that you had in mind?

Just a normal right-angle triangle.

 

[uniquegirl]

Please, see:
https://www.physicsclassroom.com/class/vectors/Lesson-1/Vectors-and-Direction

Could you show us the “as shown in the diagram”.

It is the vector diagram i have attached :)

 

[TSny]

Just a normal right-angle triangle.

Here is your drawing

There are no right triangles indicated in the drawing. Can you post an updated diagram which shows the particular right triangle that you used to set up your expression for $\sin 25^o$?

If you did not use a right triangle, can you explain how you arrived at $\sin 25^o = \large \frac{v_n}{25}$?

 

[uniquegirl]

I just used trigonometry because that is what you use to find the horizontal and vertical velocities. So it was just a guess. Are you allowed to tell me which equation would be best fit in this situation or would I have to figure that out?

 

[uniquegirl]

Is velocity=distance/time a better formula? But because I'm not given a time, I'm a bit confused

 

[Delta2]

You didn't apply the laws of trigonometry correctly.

 

[TSny]

I just used trigonometry because that is what you use to find the horizontal and vertical velocities.

Can you explain how you used trigonometry?

So it was just a guess.

We want to avoid guessing.

Are you allowed to tell me which equation would be best fit in this situation or would I have to figure that out?

It would not really help you if I told you the equation. If I did, what would you do the next time you have a similar, but somewhat different problem? It's essential that you learn to figure it out using basic information that you have learned.

I'm sure you've learned the basic trigonometry shown in this link.

Can you draw a right triangle in your drawing that has the $25^o$ angle as one of the angles in the right triangle? If you can, then you can try to identify which side is the "side adjacent" to the $25^o$ angle, etc.

 

[phinds]

Are you allowed to tell me which equation would be best fit in this situation or would I have to figure that out?

To add to what @TSny said, we are not here to GIVE you answers, we are here to help you figure out how to GET answers.

Blindly plugging things into equations is not how you get answers. You get answers by learning to understand the physics involved in problems.

 

[uniquegirl]

Can you explain how you used trigonometry?We want to avoid guessing.It would not really help you if I told you the equation. If I did, what would you do the next time you have a similar, but somewhat different problem? It's essential that you learn to figure it out using basic information that you have learned.

I'm sure you've learned the basic trigonometry shown in this link.

Can you draw a right triangle in your drawing that has the $25^o$ angle as one of the angles in the right triangle? If you can, then you can try to identify which side is the "side adjacent" to the $25^o$ angle, etc.

 

[TSny]

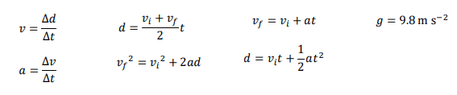
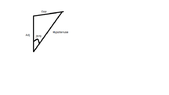
OK, that looks pretty good. The triangle should be a right triangle. Which angle in your triangle is the right angle?

 

[uniquegirl]

The one in-between opp and hyp

 

[TSny]

The one in-between opp and hyp

No. Here is a more carefully drawn diagram showing how the north and east components $V_n$ and $V_e$ are drawn.

We always construct the components by "perpendicular projection" of the (red) vector onto the axes. That is, the dotted lines meet the axes at right angles. So, we end up with right triangles.

The upper left right-triangle is the one you were essentially drawing. The right angle is the angle between the sides that are opposite and adjacent to the 25^o angle.

Can you see how to use a trig function to determine $V_n$?

 

[uniquegirl]

Would it be Vn= opp/hyp? But since the measurements for opp aren't given...

 

[Delta2]

Would it be Vn= opp/hyp? But since the measurements for opp aren't given...

Hmm, no . Can you write cos(25) and sin(25) in terms of adj,opp and hyp? Vn plays the role of adjacent side and Ve playes the role of opposite side btw in case you didn't catch that.

 

[uniquegirl]

But since Ve isn't given, would it be 25? or am I missing something?