SebastianRM
- 39
- 4
- Homework Statement
- The author says, the reaction is the ratio of SE to H. So I interpret that as R = SE/H ; however, when looking at his working, he writes R = SE/2H.
- Relevant Equations
- I understand how he derives the R expression; however, his wording throws me off as it does not match mathematically what he states. Hope this is clear. Kind regards.
I am reading a book of Fundamental Energy Systems.
The author describes the rate of change in head for a turbomachine as:
$$ \frac{1}{2}[(V_1^2-V_2^2)+(U_1^2-U_2^2)+(V_{R2}^2-V_{R1}^2)] = H =U_1V_{u1} - U_2V_{u2} $$
and the static effect as:
$$SE =(U_1^2-U_2^2)+(V_{R2}^2-V_{R1}^2) $$
However he says:
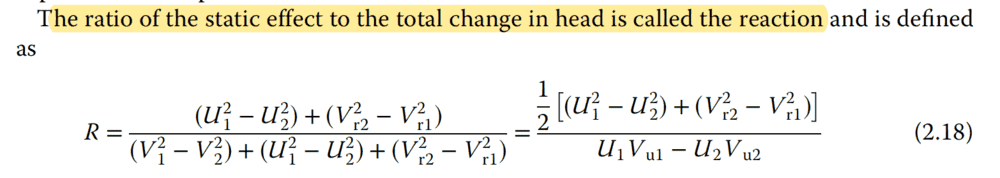
His wording states $ R = SE/H $. But he actually wrote it as we see above:
$$ R = \frac{SE}{2H} = \frac{(1/2)SE}{(1/2)2H} = \frac{(1/2)SE}{H} $$
I tried deriving his result from $ R = SE/H $ but it was not possible, I just want to make sure my conclusion is correct (R = (0.5*SE)/H ; instead of R = SE/H ) as the author does not seem to mind his own wording.
Thanks for illustrating me.
The author describes the rate of change in head for a turbomachine as:
$$ \frac{1}{2}[(V_1^2-V_2^2)+(U_1^2-U_2^2)+(V_{R2}^2-V_{R1}^2)] = H =U_1V_{u1} - U_2V_{u2} $$
and the static effect as:
$$SE =(U_1^2-U_2^2)+(V_{R2}^2-V_{R1}^2) $$
However he says:
His wording states $ R = SE/H $. But he actually wrote it as we see above:
$$ R = \frac{SE}{2H} = \frac{(1/2)SE}{(1/2)2H} = \frac{(1/2)SE}{H} $$
I tried deriving his result from $ R = SE/H $ but it was not possible, I just want to make sure my conclusion is correct (R = (0.5*SE)/H ; instead of R = SE/H ) as the author does not seem to mind his own wording.
Thanks for illustrating me.