Dumbbell Sliding on Wall: Find Speed of Weights at Equal Velocity

[walking]

A dumbbell consisting of two weights of mass m and a bar connecting them of length L is sliding down a frictionless wall and floor, with one weight on the wall and one on the floor. The dumbbell starts sliding from rest. Find the speed of the two weights when they are equal in speed.

I tried solving this problem as follows but the answer I am getting is wrong.

Here is my diagram:

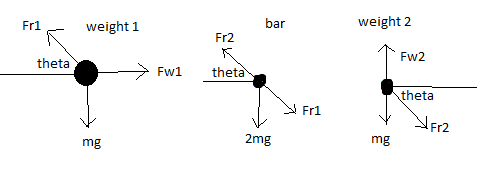
Wight 1 is the one sliding down the wall, the "bar" particle is the centre of mass of the dumbbell, and weight 2 is the one sliding on the floor.

$F_{r1}$ is the force of the bar on weight 1, $F_{w1}$ is the force of the wall, $F_{w2}$ is the normal contact force on weight 2, $F_{r2}$ is the force of the bar on weight 2. The directions of these forces was worked out by considering the direction of the net force acting on each weight. Theta is the angle that the bar makes with the horizontal at time t.

I found the following equations by resolving forces, and for the bar, using the fact that $\mathbf{F}_{ext}=M\mathbf{a}_{cm}$:

$(F_{r1}-F_{r2})\cos \theta = ma_2$

$(F_{r1}-F_{r2})\sin \theta - -2mg - ma_1$

$F_{r2}\cos \theta = ma_2$

$F_{r1}\sin \theta - mg = ma_1$

I solved these to get $a_1=-\frac{5g}{3}$ and $a_2=-\frac{l}{h}\frac{g}{3}$ where $l$ is the component of the bar in the x direction and h is its component in the y direction, both at time t.

Also, based on the definitions of h and l, I got $h^2+l^2=L^2$ which I differentiated with respect to time (since h and l are variable) to get $h\frac{dh}{dt}+l\frac{dl}{t}=0$. Now I noted that the derivatives in this equation are the speeds of the weights, ie $\frac{dh}{dt}=v_1$ and $\frac{dl}{dy}=v_2$, since these are the rates at which the weights slide on the wall and floor respectively. Also, the signs are correct because h is getting smaller which agrees with the fact that $v_1$ is negative, and similarly for the $v_2$ equation.

Now when the speeds are equal, let that speed be $v>0$. Then $v_1<0$ and so $v_1=-v$, while $v_2=v$. Plugging into the derivative equation and simplifying we get $h=l$. So by the pythagorean equation we get $h=l=\frac{L}{\sqrt{2}}$.

Now differentiating the pythagorean equation again we get $(\frac{dh}{dt})^2+h\frac{d^2h}{dt^2}+(\frac{dl}{dt})^2+l\frac{d^2l}{dt^2}=0$, ie $2v^2+\frac{L}{\sqrt{2}}a_1\frac{L}{\sqrt{2}} a_2=0$, and using the values of $a_1,a_2$ we got at the beginning, this becomes $2v^2=\frac{L}{\sqrt{2}}2g$ or finally $v=\sqrt{\frac{g}{\sqrt{2}}}\sqrt{L}$, which is the wrong answer. I am not sure where I went wrong.

The actual problem and solution are on page 620 here:

https://archive.org/details/TiplerPhysics5Ed.CompleteSolutions1/page/n617
(The answer given there is $v=\sqrt{g(1-\frac{1}{\sqrt{2}})}\sqrt{L}$ which is very similar to what I got.)

 

[BvU]

Hi, I read your expose a few times and have trouble understanding what you do. You use symbols you don't explain and explain symbols you don't use. You say

I solved these

without showing what you did and come with an answer independent of $\theta$.

In your diagram

there is definitely no force of $2mg$ working on the center (in addition to the two $mg$ on the weights). That center is massless and describes a quarter circle during the slide down. Nothing useful for solving the problem there.

You 'use' a fact ${\bf F}_{ext} = M {\bf a}_{cm}$ where upper case $M$ is what ? and ${\bf F}_{ext} \$ is what ? and ${\bf a}_{cm}\$ is what ?

$F_{r1}$ is working on weight 1 only, it can never occur in something like $(F_{r1}-F_{r2})\cos \theta = ma_2$, presumably the equation of motion for weight 2.

All the above appears a bit negative, sorry.

To be a bit more constructive:
write down your assumptions (bar massless, weights pointlike (i.e. no rotation inertia))
explicitly write down what you know (the two $mg$, and what else ? Is e.g. $\vec F_{r1} = - \vec F_{r2}$ ? )

The solution manual works with energy, you want to use Newton -- I suppose it can be done (didn't check)

 

[PeroK]

I'm struggling to see the relevance of forces. It asks about speed, not acceleration.

PS I wonder if the answer that "by symmetry" the speeds must be the same when the angle is $45°$ would be acceptable?

PPS that must be true geometrically however the dumbells are moved. Hence completely independent of the forces involved.

PPPS unless the speed is zero of course!

 

[walking]

Hi, I read your expose a few times and have trouble understanding what you do. You use symbols you don't explain and explain symbols you don't use. You say
without showing what you did and come with an answer independent of $\theta$.

In your diagram
View attachment 245616
there is definitely no force of $2mg$ working on the center (in addition to the two $mg$ on the weights). That center is massless and describes a quarter circle during the slide down. Nothing useful for solving the problem there.

You 'use' a fact ${\bf F}_{ext} = M {\bf a}_{cm}$ where upper case $M$ is what ? and ${\bf F}_{ext} \$ is what ? and ${\bf a}_{cm}\$ is what ?

$F_{r1}$ is working on weight 1 only, it can never occur in something like $(F_{r1}-F_{r2})\cos \theta = ma_2$, presumably the equation of motion for weight 2.

All the above appears a bit negative, sorry.

To be a bit more constructive:
write down your assumptions (bar massless, weights pointlike (i.e. no rotation inertia))
explicitly write down what you know (the two $mg$, and what else ? Is e.g. $\vec F_{r1} = - \vec F_{r2}$ ? )

The solution manual works with energy, you want to use Newton -- I suppose it can be done (didn't check)

Not negative at all, it was my fault for being unclear, sorry.

I will try to clarify what I did but I may still miss some things, please just let me know and I will describe them.

The outline of my solution is basically using NII on weight 1, then on weight 2, and finally by using NII on the system as a whole by considering the dumb-bell as a particle and using the fact that the centre of mass of a system moves like "a particle under an external force". The formula I learned for the latter is $F_{ext}=Ma_{cm}$ where $F_{ext}$ is the net external force on the system, $M$ is total mass and $a_{cm}$ is the acceleration of the centre of mass. So the centre of mass of the system can be modeled as having mass 2m as I did. (I am assuming the bar is massless.)

Regarding the forces, I have already defined them so I don't see what is confusing. The force of the bar on weight 1 is $F_{r1}$, and by NIII the weight acts on the bar with the same magnitude force $F_{r1}$ but in the opposite direction as shown in the diagram. I hope the other forces are clearer now that I have explained how I was using the centre of mass.

I eliminated the angle simply by adding equations together etc. I don't have my notes at the moment but it is a simple case of solving simultaneous equations. I am sure I didn't make a mistake during this step. The $F_{r1}-F_{r2}$ etc is from resolving in the x and y directions for the centre of mass of the system, using $F_{ext}=Ma_{cm}=ma_1+ma_2$ where the forces and accelerations are vectors. Then I simply equated vector components of both sides, noting that $a_1$ (the acceleration downwards of weight 1) doesn't have an x component and $a_2$ doesn't have a y component. This is how I got the simple "$F_{r1}-F_{r2}$" equations. All the equations are from resolving the forces in the diagram I provided.

My assumptions:
The bar is massless and thin. The weights are not point-like and I don't need to assume this in my solution. I use the x and y components of the length L of the bar regardless of how big the weights are. The weights are spherical

Please let me know if anything else needs to be clarified, I really am not seeing why the answer I got is incorrect.

I just wanted to say that my solution cannot be completely wrong considering how close the final answer is to the official solution's answer. I am simply trying to understand where I went wrong.

 

[PeroK]

I solved these to get $a1=-\frac{5g}{3}$ and $a2=-\frac{l}{h}\frac{g}{3}$ where l is the component of the bar in the x direction and h is its component in the y direction, both at time t.

This can't be right. $a_1$ is constant, doesn't depend on $l$ and is greater than $g$?

PS You should be able to see that $a_1 \rightarrow 0$ as $h \rightarrow L$; and $a_1 \rightarrow g$ as $h \rightarrow 0$. That should be a sanity check on your equation for $a_1$.

 

[BvU]

I have already defined them so I don't see what is confusing

I understand that $F_{ext}=Ma_{cm}=ma_1+ma_2$ but I don't see $F_{ext}$ reappearing. Do you understand it is definitely is NOT equal to $2mg$ ? Do you understand that $F_{r1}$ does not act on weight 1 and you simply can not write $(F_{r1}-F_{r2})\cos \theta = ma_2$ ?

I hope the other forces are clearer

I can fill in a lot of things; the point I tried to make is that you should be much more consistent in defining and using variables. Then work with the relevant equations until you have something with the searched for unknown on one side and only knowns on the other.

The weights are not point-like and I don't need to assume this in my solution

You certainly do. As I said, rotational inertia must be ignored to solve this one and come up with the same answer as the book did.

Do you understand and agree with the energy-based solution ? So your plan is to find the same answer using Newton equations of motion, right ?

That means setting up equations for the acceleration (as a function of ? )
Then differentiating wrt ? and finding when that is zero.

Or did you have some other plan in mind ?

 

[PeroK]

Do you understand and agree with the energy-based solution ? So your plan is to find the same answer using Newton equations of motion, right ?

That means setting up equations for the acceleration (as a function of ? )
Then differentiating wrt ? and finding when that is zero.

Or did you have some other plan in mind ?

... What can you say about the accelerations when the speeds are equal? Maybe nothing definite?

 

[BvU]

Ah, thanks Perok -- I did not re-read post #1 and wrongy thought it was asking for maximum speeds of the weights.

New solving plan:

Set up equations for the acceleration (as a function of ? )
Then derive the velocities, also as a function of ? and finding when they are equal

Daunting ...

 

[walking]

Ah, thanks Perok -- I did not re-read post #1 and wrongy thought it was asking for maximum speeds of the weights.

New solving plan:

Set up equations for the acceleration (as a function of ? )
Then derive the velocities, also as a function of ? and finding when they are equal

Daunting ...

Why does conservation of energy (as used in the official solution) work in this situation? What is the condition for it to be a valid application?

Edit: I think I am confused by the use of CoE because I was taught that the condition was "all forces that do work are internal and conservative" (basically the exact wording of the Tipler & Mosca book I am using - including "internal" and "conservative"). However, I am not seeing how all forces of the earth-dumbbell-wall-floor system that do work are internal and conservative. Ok, they are internal because we have basically included everything in our system, from the Earth to the wall etc. But what about conservative? How do we quickly see that the contact force of the connecting bar on the top ball is conservative for example? I am sure I am over-complicating things.

Edit 2: Also, why I am not easily seeing the "by symmetry" argument of the official solution (ie "by symmetry", the speeds are equal at 45 degrees. I am not seeing this, mainly because it doesn't seem to be a complete symmetry, since one ball slides on a wall, the other on the floor, and it isn't 100% clear to me that this allows a symmetry argument - as in mathematics for example, where it is usually obvious). In any case, I have shown how to easily prove this using $h^2+l^2=L^2$ and differentiation, which shows that the speeds are equal when $h=l=\frac{L}{\sqrt{2}}$.

 

[PeroK]

Why does conservation of energy (as used in the official solution) work in this situation? What is the condition for it to be a valid application?

Edit: I think I am confused by the use of CoE because I was taught that the condition was "all forces that do work are internal and conservative" (basically the exact wording of the Tipler & Mosca book I am using - including "internal" and "conservative"). However, I am not seeing how all forces of the earth-dumbbell-wall-floor system that do work are internal and conservative. Ok, they are internal because we have basically included everything in our system, from the Earth to the wall etc. But what about conservative? How do we quickly see that the contact force of the connecting bar on the top ball is conservative for example? I am sure I am over-complicating things.

Edit 2: Also, why I am not easily seeing the "by symmetry" argument of the official solution (ie "by symmetry", the speeds are equal at 45 degrees. I am not seeing this, mainly because it doesn't seem to be a complete symmetry, since one ball slides on a wall, the other on the floor, and it isn't 100% clear to me that this allows a symmetry argument - as in mathematics for example, where it is usually obvious). In any case, I have shown how to easily prove this using $h^2+l^2=L^2$ and differentiation, which shows that the speeds are equal when $h=l=\frac{L}{\sqrt{2}}$.

Energy is conserved (for a system) if no energy is lost or gained by the system in question. That is the point of defining gravitational potential energy (GPE). There is no conservation of Kinetic Energy (KE) of the dumbbell. So, you have to explain where the KE comes from. You do that by defining the GPE (of the dumbbell). Then you have conservation of KE + GPE.

You can look at conservation of energy more generally; but, in the case of motion in the Earth's gravitational field, near the surface, that's what conservation of energy amounts to.

There are two obvious ways that energy can be lost by the dumbell: air resistance (where energy is lost to heat in the air and of the dumbbell); and, friction between the dumbbell and the walls.

If we neglect these factors, then we have conservation of energy (GPE + KE) in this case.

Regarding the symmetry argument. You can prove it quite easily:

$h = L\sin \theta$ and $l = L\cos \theta$

If you differentiate those, then you'll find that $\dot h = \dot l$ when $\cos \theta = \sin \theta$ or $\dot \theta = 0$.

 

[PeroK]

Why does conservation of energy (as used in the official solution) work in this situation? What is the condition for it to be a valid application?

Edit: I think I am confused by the use of CoE because I was taught that the condition was "all forces that do work are internal and conservative" (basically the exact wording of the Tipler & Mosca book I am using - including "internal" and "conservative").

I don't really understand that definition. In this case, the gravitational force is external; but, by defining the GPE associated with it, we have conservation of energy.

 

[BvU]

[edit] PeroK was faster - nevertheless:

Ok, they are internal because we have basically included everything in our system, from the Earth to the wall etc

I don't think we did: we do not let the Earth turn faster or slower because this dumbbell is pushing against the wall. Nor do we let the Earth move up because the dumbbell goes down.

Instead we use the fact that no mechanical energy is lost (no friction) and the gravitational field of the Earth is conservative (move something up and down -- when it ends up at he same height the potential energy from gravity is the same as at the start). So in a sense we did include the work that gravity is doing by taking the potential energy from gravity into account fr the dumbbell..

Book solution wording confuses you (book is to be blamed !) : in this scenario the increase of kinetic energy is equal to the decrease in potential energy. That way the system is extended to include the (conservative) graviational force field. We use it in exercises when balls describe parabolic trajectories.

My reason to jump on your $F_{ext}=Ma_{cm}$ is that external forces include the normal forces that the wall and the floor exert on the two masses. They do no work (for the wall normal force there is no force component in the direction of motion of the contact point with the wall -- for the floor similar). But the forces are not zero, so you don't know $\sum F_{ext}$.

But what about conservative? How do we quickly see that the contact force of the connecting bar on the top ball is conservative for example?

It doesn't cause motion wrt the center of mass

If I use your diagram in post #1 (erasing the middle one) and explain that
$\vec a_1$ is the acceleration of weight 1
$\vec a_2$ is the acceleration of weight 2
$\vec a_1$ is in the vertical direction: $\vec a_1 = (0, a_1)$
$\vec a_2$ is in the horizontal direction: $\vec a_2 = (a_2, 0)$
I get the following equations $$\begin{align*}
&F_{r1}\cos\theta & + F_{w1}& = {}& 0 \\
&F_{r1}\sin\theta & + mg & = {}& ma_1 \\
&F_{r2}\cos\theta & & = {}& ma_2 \\
&F_{r2}\sin\theta & + mg & ={} & 0 \end {align*}$$
(the last one eliminates $F_{r2}$)
We assume $F_{r1}$ and $F_{r2}=0$ are both acting in the direction of the bar which needs an argument.

To get anywhere with this, we need more: we have four equations with 6 unknowns. So you need something like $F_{r1}+F_{r2}=0$ which needs an argument too, plus e.g. a relationship between $a_1$ and $a_2$ (without intrducing new unknowns, of course).

To do this with Newton equations of motion doesn't look promising to me, but I would like to be proven wrong.

(Euler Langrange might be easier, didn't look at that).