Can't understand 2 pulley 3 masses problem

[TissueCulture]

Homework Statement

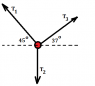
System is in equilibrium. 1 mass known: 79.4 kg (or 778.6 N) and 2 other unknown. Other masses unaccounted for. Everything friction-less. The Tensions are unknown also.

Homework Equations

∑F = 0
∑Fx = -T1*cos135 + -T3*cos37 = 0
∑Fy = (-T1*sin135 - m1g) + (-T3*sin37 - m3g) + T2 - 778.6 N = 0

The Attempt at a Solution

I don't have any idea how to comprehend this problem. Of course I am missing something but I don't know how to ''think'' the problem from the get go. Any pointers would be very appreciated, I have tried to figure it out for the last hours...The T1 and T3 arrows should be parallel to the rope on the drawing

 

[TSny]

The key is to consider the forces acting on the red knot where the three strings meet. The knot is in static equilibrium. Below is a figure of the knot and the three strings. Use that as the beginning of a free-body diagram of the knot. You should draw the force vectors acting on the knot and label them. Be sure to put arrow heads on the force vectors to indicate the directions of the forces.

 

[TissueCulture]

So if I understand correctly, you mean that I should consider that T1,T2 and T3 vectors are pulling away from the red knot instead of towards it? Wouldn't that make them go in the same direction as the m1g, m2g and m3g vectors? Or is it an error on my part to consider the masses of the objects as vectors instead of mere units of mass? Thank you very much for your help!

 

[TSny]

Yes, the three tension forces acting on the knot all point away from the knot along the strings. There are no other forces acting on the knot.

 

[TissueCulture]

One thing I can't get my head around is if I must substract the masses with both ∑Fx and ∑Fy

∑Fx = -T1*cos135 - m1g + T3*cos37 + m3g = 0
∑Fy = (T1*sin135 + m1g) + (T3*sin37 + m3g) - T2 - 778.6 N = 0

Are these valid to start the problem? I have a hard time understanding how to ''translate'' the force vectors of the free-body diagram into mathematically sound equations for both X and Y axis. Thanks for your help anyone!

 

[TSny]

There are only three forces acting on the knot: T₁, T₂, and T₃. So when you write out ∑F_x and ∑F_y, you should only use these three forces.

When you write the x-component of T₁, you should write it as T₁cos135^o and not as -T₁cos135^o. If you calculate cos135^o, you will see that it is a negative number. So, T₁cos135^o is already negative. You shouldn't add an extra negative sign in front.

However, if they had specified the angles as shown below, then the x-component of T₁ would be written with a negative sign as
-T₁cos45^o

 

[TissueCulture]

Thank you very much! in fact, both angles had to be measured in real life but I thought I had to consider the angle in relation to the positive X axis (I don't know if this is clear), so I ended up with 135 degrees. However, I suppose it is more logical or easier to go with 45 degrees now that you told me this...! What got me bugged is how I am including the weights in the equations (m1g, m2g (778.6N) and m3g). Does it seem like I'm on the right track?

 

[TSny]

Try to write out ∑F_x = 0 and ∑F_y = 0 for the knot. The only forces that should appear are the x or y components of the three tension forces.

However, you can then proceed to relate the tension forces to the weights of the three objects at the other end of the ropes. To do this, construct a separate free body diagram for each of the three objects and apply the condition for equilibrium.

You can assume that the tension at one end of a rope is equal to the tension at the other end of that rope.

 

[TissueCulture]

Hi again! Here is what I found so far, if correct I only have one other question!

∑F = T1 + T2 + T3 (with vector arrows)
∑Fx = -T1cos45 + T3cos37 = 0
∑Fy = T1sin45 - T2 + T3sin37 = 0

1) -T1cos45 + T3cos37 = 0
T1 = (T3cos37)/cos45 = 1,129T3

2) T3(1,129*sin45 + sin37) - T2 = 0
T3(0,7986 + sin37) - 778,6N = 0
T3(1,400) = 778,6N
T3 = 778,6N / 1,400 = 556,1 N

3) T1 = 1,129 * 556,1N = 627,8 N

If the above is OK, I just wonder if the masses for the objects are equal to double their equivalent in Newtons, so: m1 = 2*T1 (in N) ??

Thanks a lot for your help TSny! :)

 

[TSny]

Hi again! Here is what I found so far, if correct I only have one other question!

∑F = T1 + T2 + T3 (with vector arrows)
∑Fx = -T1cos45 + T3cos37 = 0
∑Fy = T1sin45 - T2 + T3sin37 = 0

1) -T1cos45 + T3cos37 = 0
T1 = (T3cos37)/cos45 = 1,129T3

2) T3(1,129*sin45 + sin37) - T2 = 0
T3(0,7986 + sin37) - 778,6N = 0
T3(1,400) = 778,6N
T3 = 778,6N / 1,400 = 556,1 N

3) T1 = 1,129 * 556,1N = 627,8 N

Your results for the tensions look correct and your work is nicely written out.

If the above is OK, I just wonder if the masses for the objects are equal to double their equivalent in Newtons, so: m1 = 2*T1 (in N) ??

I'm not sure why you would think that. Suppose you want to find m₁. Draw a free body diagram for the object with mass m₁. How many forces act on this mass? What direction do they point? Is m₁ in equilibrium? Do you know the value of any of the forces acting on m₁?

 

[TissueCulture]

What I mean to say is, I thought that a pulley divided by a factor of 2 the force necessary to lift it. I'm not sure exactly where I have read that, I cannot find it in my notes...Maybe I am mistaken! I sure know now that T1 is 627,8N but my brain seems to tell me there is more to it than simply T1 = m1 (which needs to be converted into kg). Am I just crazy?

Thanks for the encouragement by the way!

 

[TissueCulture]

Aaaah I think I get why I thought it divides the force by 2. I somehow subconsciously considered this system as a combined pulley system, with each pulley being fixed of course but the ''knot'' acting as a movable pulley, which is not the case!

I now assume that it is clearly T1 = m1, since :
'' There is a force (tension) on the rope that is equal to the weight of the object.
This force or tension is the same all along the rope. In order for the weight
and pulley (the system) to remain in equilibrium, the person holding the end
of the rope must pull down with a force that is equal in magnitude to the
tension in the rope. For this pulley system, the force is equal to the weight, as
shown in the picture. The mechanical advantage of this system is 1'' I cannot post the picture but it shows a simple pulley with a weight attached. Found this online.

 

[TSny]

Yes. However, keep in mind that mass is not the same as weight. So, you would not say that T₁ = m₁. Otherwise, I think your reasoning is good!

 

[TissueCulture]

Yes I was about to add that in fact, the force being already known, it would rather go like: T1 = m1*g → M1 = T1/g

Which gives the mass!

Thanks a lot again for your help!

 

[TSny]

Yes I was about to add that in fact, the force being already known, it would rather go like: T1 = m1*g → M1 = T1/g

Which gives the mass!

Yes, good work.