z3phyr
- 4
- 0
Hi there
I've encounted a problem in which I'm required to calculate the total capacitance between the end of a cylindrial rod and an infinite ground plane.
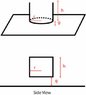
I've attached a schematic drawing here. The gap between the rod if far smaller than the diameter.
http://picasaweb.google.com/lh/photo/igUbKtbtX7AiyLX5tsQFQg?feat=directlink
The part I can't figure out is the fringing capacitance from the sidewalls to the ground plane. I wonder if anybody has seem this problem before or know of any analytical/semi-analytical formula for estimating the fringing capacitance? I've done some numerical simulation with Ansoft Maxwell and I can definitely see a fringing field contribution that can not be neglected.
Greatly appreciated!
I've encounted a problem in which I'm required to calculate the total capacitance between the end of a cylindrial rod and an infinite ground plane.
I've attached a schematic drawing here. The gap between the rod if far smaller than the diameter.
http://picasaweb.google.com/lh/photo/igUbKtbtX7AiyLX5tsQFQg?feat=directlink
The part I can't figure out is the fringing capacitance from the sidewalls to the ground plane. I wonder if anybody has seem this problem before or know of any analytical/semi-analytical formula for estimating the fringing capacitance? I've done some numerical simulation with Ansoft Maxwell and I can definitely see a fringing field contribution that can not be neglected.
Greatly appreciated!
Attachments
Last edited by a moderator: