Capacitor: surface charge densities

[unscientific]

Homework Statement

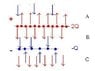
Given a capacitor, top plate with charge 2Q, bottom plate -Q: Find surface charge densities of all four surfaces and E-fields everywhere.

Homework Equations

The Attempt at a Solution

I start off with the general case of top plate having charge Q₁, bottom plate Q₂. Inner surfaces of capacitor get their charge densities distorted more. (Zero distortion when plates are very far away; equal charge distributed on inner and outer surfaces)

Inner and outer top surfaces charge density distorted by sigma, while bottom inner and outer surfaces distorted by gamma$$\sigma_1 = \frac{Q_1}{2A} - \delta, E_1 = \frac{1}{2\epsilon_0}(\frac{Q_1}{2A} - \delta)$$
$$\sigma_2 = \frac{Q_1}{2A} + \delta, E_2 = \frac{1}{2\epsilon_0}(\frac{Q1}{2A} + \delta)$$
$$\sigma_3 = -\frac{Q_2}{2A} - \gamma, E_3 = \frac{1}{2\epsilon_0}(-\frac{Q2}{2A} - \gamma)$$
$$\sigma_4 = -\frac{Q_2}{2A} + \gamma, E_4 = \frac{1}{2\epsilon_0}(-\frac{Q2}{2A} + \gamma)$$

Electric fields at regions

$$E_A = -E_1 - E_2 + E_3 + E_4 = \frac {1}{2\epsilon_0}(-\frac{Q_1}{A}-\frac{Q_2}{A})$$
$$E_B = E_1 - E_2 + E_3 + E_4 = \frac{1}{2\epsilon_0}(-2\delta -\frac{Q_2}{A}) = 0$$
$$E_C = E_1 + E_2 + E_3 + E_4 = \frac{1}{2\epsilon_0}(\frac{Q_1}{A}-\frac{Q_2}{A})$$
$$E_D = E_1 + E_2 -E_3 + E_4 = \frac{1}{2\epsilon_0}(\frac{Q_1}{A} + 2\gamma) = 0$$
$$E_E = E_1 + E_2 - E_3 - E_4 = \frac{1}{2\epsilon_0}(\frac{Q_1}{A} + \frac{Q_2}{A})$$

Answers
$$\sigma_1 = \frac{Q}{2A}, E_1 = \frac{Q}{4A\epsilon_0}$$
$$\sigma_2 = \frac{3Q}{2A}, E_2 = \frac{3Q}{4A\epsilon_0}$$
$$\sigma_3 = \frac{3Q}{2A}, E_3 = \frac{3Q}{4A\epsilon_0}$$
$$\sigma_4 = \frac{-Q}{2A}, E_4 = \frac{-Q}{4A\epsilon_0}$$

These answers are wrong, as the inner plates should have equal but opposite charge densities, the outer plates will have exactly same charge densities. I checked similar questions online.

I'm guesssing the charge densities should be (from top to bottom surfaces): +1/2, +3/2, -3/2, +1/2.

 

[ehild]

Homework Statement

Given a capacitor, top plate with charge 2Q, bottom plate -Q: Find surface charge densities of all four surfaces and E-fields everywhere.I'm guesssing the charge densities should be (from top to bottom surfaces): +1/2, +3/2, -3/2, +1/2.

Your guess is correct, but I can not follow your derivation. The electric field of a surface charge on a metal surface is σ/ε₀ outward, not the half.

Imagine you have 2Q charge arranged evenly along a plane at the position of the upper plate of the capacitor, and -Q charge along a plane at he position of the bottom plate. Determine the electric field above the planes, between them and below.

If you know the electric fields you can place the plates of the capacitor back. You know that the surface charge density on a metal surface is equal to ε₀E. Knowing E, you can determine the surface charge densities at both sides of both capacitor plates.

 

[unscientific]

Your guess is correct, but I can not follow your derivation. The electric field of a surface charge on a metal surface is σ/ε₀ outward, not the half.

Imagine you have 2Q charge arranged evenly along a plane at the position of the upper plate of the capacitor, and -Q charge along a plane at he position of the bottom plate. Determine the electric field above the planes, between them and below.

If you know the electric fields you can place the plates of the capacitor back. You know that the surface charge density on a metal surface is equal to ε₀E. Knowing E, you can determine the surface charge densities at both sides of both capacitor plates.

I tried that, didn't work:

Gauss's Law on inner plates:
$$\frac{\sigma_2}{2\epsilon_0} = \frac{-\sigma_3}{2\epsilon_0}$$

Conservation of Charge on plates:
$$A(\sigma_1 + \sigma_2) = 2Q$$
$$A(\sigma_3 + \sigma_4) = -Q$$I only end up with 3 equations..

 

[unscientific]

Your guess is correct, but I can not follow your derivation. The electric field of a surface charge on a metal surface is σ/ε₀ outward, not the half.

Imagine you have 2Q charge arranged evenly along a plane at the position of the upper plate of the capacitor, and -Q charge along a plane at he position of the bottom plate. Determine the electric field above the planes, between them and below.

If you know the electric fields you can place the plates of the capacitor back. You know that the surface charge density on a metal surface is equal to ε₀E. Knowing E, you can determine the surface charge densities at both sides of both capacitor plates.

I have come up with another equation, by trial and error -- Consider the field inside the top plate = 0

Case 1: top outer surface (-), bottom outer surface (+)
$$\sigma_1 - \sigma_2 - \sigma_3 -\sigma_4 = 0$$

Case 2: top outer surface (+), bottom outer surface (-)
$$\sigma_1 - \sigma_2 - \sigma_3 -\sigma_4 = 0$$

Case 3: top outer surface (+), bottom outer surface (+)
$$\sigma_1 - \sigma_2 - \sigma_3 -\sigma_4 = 0$$

Case 4: top outer surface (-), bottom outer surface (-)
$$\sigma_1 - \sigma_2 - \sigma_3 -\sigma_4 = 0$$

They all give the same relation. This equation with the three above, we can solve for them.

 

[ehild]

Try to work with the field lines. Every positive charge q is the source of q/ε₀ field lines, and every negative, -q charge is the sink of q/ε₀ field lines.

Imagine two planar arrangement of charges, 2Q on the upper plane and -Q on the bottom plane. Apply the method of superposition. Both planes contribute to the field in every domain A, B ,C and the net field is the sum of these contributions.
You have 2Q/ε₀ field lines, emerging from the upper plane symmetrically at both sides of the plane, both upward and downward. Take upward positive. The downward field lines penetrate to both B and C. So the upper plane contributes to the electric field in domain A with Q/(Aε₀) , and with -Q/(Aε₀) between the planes (B) and also in domain C.
The other, negative plane of charges contributes to the field with Q/(2Aε₀) in domain C, and with -Q/(2Aε₀) in both B and A.

Adding these contributions, you get:

E_A=Q/(Aε₀)-Q/(2Aε₀)=1/2 Q/(Aε₀)

E_B=-Q/(Aε₀)-Q/(2Aε₀)=-3/2 Q/(Aε₀)

E_C...

Can you proceed?

Now you place the metal plates in the position of the planes - it does not change the fields in A, B, C. The magnitude of the surface charge density is |E|ε₀ on each surfaces.

ehild

 

[unscientific]

Try to work with the field lines. Every positive charge q is the source of q/ε₀ field lines, and every negative, -q charge is the sink of q/ε₀ field lines.

Imagine two planar arrangement of charges, 2Q on the upper plane and -Q on the bottom plane. Apply the method of superposition. Both planes contribute to the field in every domain A, B ,C and the net field is the sum of these contributions.
You have 2Q/ε₀ field lines, emerging from the upper plane symmetrically at both sides of the plane, both upward and downward. Take upward positive. The downward field lines penetrate to both B and C. So the upper plane contributes to the electric field in domain A with Q/(Aε₀) , and with -Q/(Aε₀) between the planes (B) and also in domain C.
The other, negative plane of charges contributes to the field with Q/(2Aε₀) in domain C, and with -Q/(2Aε₀) in both B and A.

Adding these contributions, you get:

E_A=Q/(Aε₀)-Q/(2Aε₀)=1/2 Q/(Aε₀)

E_B=-Q/(Aε₀)-Q/(2Aε₀)=-3/2 Q/(Aε₀)

E_C...

Can you proceed?

Now you place the metal plates in the position of the planes - it does not change the fields in A, B, C. The magnitude of the surface charge density is |E|ε₀ on each surfaces.

ehild

I have solved it using the four equations above, thank you very much for your help too!