SUMMARY
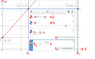
This discussion focuses on calculating the relative motions of a car and a truck during an acceleration phase. The car accelerates from 20 m/s to 25 m/s with a constant acceleration of 1.8 m/s², taking 2.78 seconds to reach its maximum speed, covering a distance of 62.5 meters. The truck, traveling at a constant speed of 18 m/s, covers 50 meters in the same time frame, resulting in the car being 37.5 meters behind the truck at the end of the acceleration. The participants emphasize the importance of using equations of motion for accurate calculations rather than relying solely on trial and error.
PREREQUISITES
- Understanding of basic kinematics, including acceleration and velocity.
- Familiarity with equations of motion, specifically
s = ut + 0.5at².
- Ability to manipulate algebraic equations to solve for unknowns.
- Knowledge of graphing distance versus time for motion analysis.
NEXT STEPS
- Study the equations of motion in detail, focusing on
s = ut + 0.5at² and v_f = v_i + at.
- Learn how to derive average speed during acceleration phases.
- Practice solving relative motion problems involving multiple objects.
- Explore graphical representations of motion to visualize distance versus time relationships.
USEFUL FOR
Students studying physics, educators teaching kinematics, and anyone interested in understanding relative motion in dynamic systems.