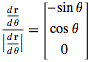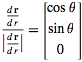shreddinglicks
- 225
- 7
Homework Statement
I want to convert R = xi + yj + zk into cylindrical coordinates and get the acceleration in cylindrical coordinates.
Homework Equations
The Attempt at a Solution
I input the equations listed into R giving me:
R =
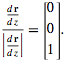
Apply chain rule twice:
The final answer is:
How do I get this final answer? It looks like the terms with sin were dropped. How does this happen?
Attachments
-
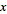 Inline31.gif173 bytes · Views: 761
Inline31.gif173 bytes · Views: 761 -
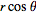 Inline33.gif1.1 KB · Views: 528
Inline33.gif1.1 KB · Views: 528 -
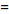 Inline38.gif162 bytes · Views: 532
Inline38.gif162 bytes · Views: 532 -
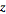 Inline37.gif273 bytes · Views: 492
Inline37.gif273 bytes · Views: 492 -
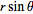 Inline36.gif1 KB · Views: 538
Inline36.gif1 KB · Views: 538 -
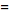 Inline35.gif162 bytes · Views: 526
Inline35.gif162 bytes · Views: 526 -
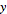 Inline34.gif277 bytes · Views: 473
Inline34.gif277 bytes · Views: 473 -
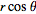 Inline33.gif1.1 KB · Views: 525
Inline33.gif1.1 KB · Views: 525 -
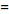 Inline32.gif162 bytes · Views: 748
Inline32.gif162 bytes · Views: 748 -
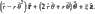 Inline212.gif2 KB · Views: 481
Inline212.gif2 KB · Views: 481 -
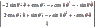 Inline209.gif3.2 KB · Views: 488
Inline209.gif3.2 KB · Views: 488 -
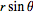 Inline36.gif1 KB · Views: 474
Inline36.gif1 KB · Views: 474