corochena
- 16
- 0
[SOLVED] Center of Mass of compound cylinder
I have this problem. I have a cylinder filled with two liquids of different densities and not able to mix up (like oil and water). I have to fill the cilynder in such a way so that the center of mass will be located as low as possible. For example, mercury and water, cylinder radius = 1cm, height = 10cm. How much mercury and water should I use? What would be the location of the center of mass. Note: The cylinder must be filled in completely. Give a response in function of the densities of the fluids.
I have this problem. I have a cylinder filled with two liquids of different densities and not able to mix up (like oil and water). I have to fill the cilynder in such a way so that the center of mass will be located as low as possible. For example, mercury and water, cylinder radius = 1cm, height = 10cm. How much mercury and water should I use? What would be the location of the center of mass. Note: The cylinder must be filled in completely. Give a response in function of the densities of the fluids.
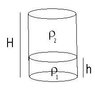

 .
.