- #1
zenterix
- 774
- 84
- Homework Statement
- A homogenous spherical shell of radius ##a## is cut by one nappe of a right circular cone whose vertex is at the center of the sphere. If the vertex angle of the cone is ##\alpha##, where ##0<\alpha<\pi##, determine (in terms of ##a## and ##\alpha## the center of mass of the portion of the spherical shell that lies inside the cone.
- Relevant Equations
- ##\iint_S f(x,y,z)dS##
I am asking this question because my solution does not seem to match the solution at the end of the book (Apostol Vol II, section 12.10, problem 9).
Here is my attempt to solve this problem.
If our coordinate system is chosen such that the z-axis lines up with the axis of the cone then by symmetry the ##x## and ##y## coordinates of the center of mass will both be zero.
All that is left is to calculate the z-coordinate of the center of mass.
Using spherical coordinates, the cone is ##\theta=\alpha/2## and the sphere is ##\rho=a##.
The parameterized equation for the sphere is ##\vec{r}=\langle a\sin{\theta}\cos{\phi}, a\sin{\theta}\sin{\phi}a\cos{\theta}\rangle##.
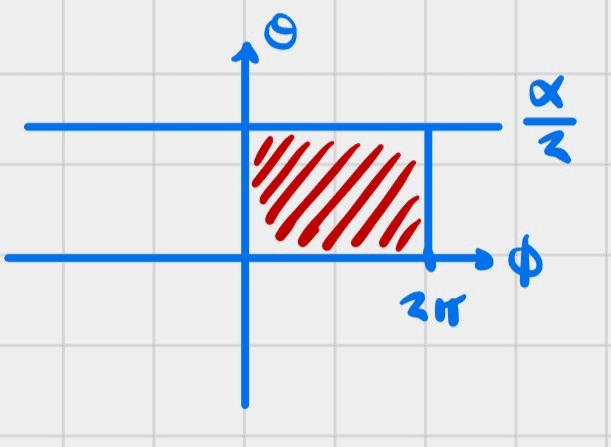
The portion inside the cone is the red area below
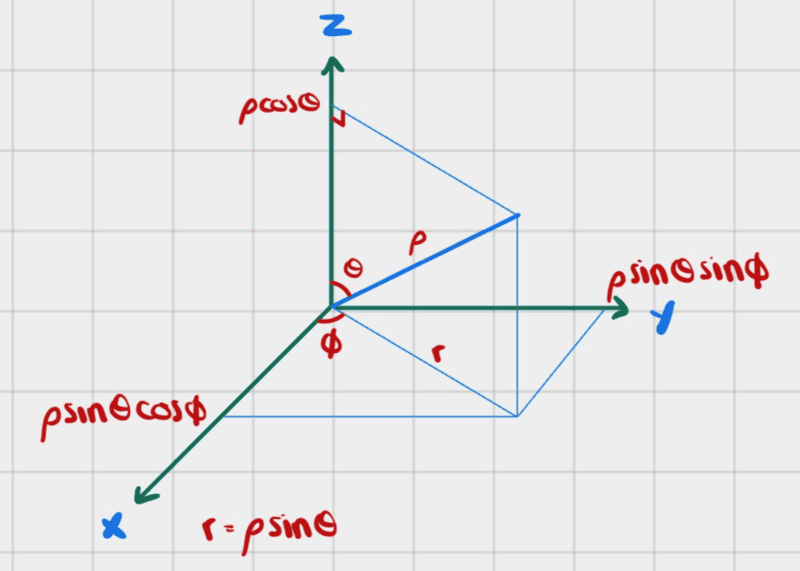
Just to be clear about the coordinate system, I am using spherical coordinates defined as follows
Now, the spherical shell has a constant density of ##d(x,y,z)=\frac{M}{4\pi a^2}##.
Let's define ##f(x,y,z)=z\cdot d(x,y,z)##.
Then our calculation of ##z_{cm}## is
$$z_{cm}=\frac{\int\int_S f(x,y,z) dS}{\int\int_S d(x,y,z)dS}$$
$$=\frac{\int\int_S f(\vec{r}(\theta,\phi))\cdot \lVert \frac{d\vec{r}}{d\theta}\times\frac{d\vec{r}}{d\phi} \rVert d\theta d\phi}{\int\int_S d(\vec{r}(\theta,\phi)) \lVert \frac{d\vec{r}}{d\theta}\times\frac{d\vec{r}}{d\phi} \rVert d\theta d\phi}$$
The denominator is
$$\frac{M}{4\pi a^2}\int_0^{2\pi}\int_0^{\alpha/2} a^2\sin{\theta}d\theta d\phi$$
$$=\frac{M(1-\cos{(\alpha/2)}}{2}$$
And the numerator is
$$\frac{M}{4\pi a^2}a^3\int_0^{2\pi}\int_0^{\alpha/2} \sin{\theta}\cos{\theta} d\theta d\phi$$
$$=\frac{Ma\sin^2{(\alpha/2)}}{4}$$
Thus when we put numerator and denominator together we get
$$\frac{\frac{Ma\sin^2{(\alpha/2)}}{4}}{\frac{M(1-\cos{(\alpha/2)}}{2}}$$
$$=\frac{a\sin^2{(\alpha/2)}}{2(1-\cos{(\alpha/2)})}$$
However, it seems that either I have made a mistake or the solutions manual is wrong, because they have the answer
Here is my attempt to solve this problem.
If our coordinate system is chosen such that the z-axis lines up with the axis of the cone then by symmetry the ##x## and ##y## coordinates of the center of mass will both be zero.
All that is left is to calculate the z-coordinate of the center of mass.
Using spherical coordinates, the cone is ##\theta=\alpha/2## and the sphere is ##\rho=a##.
The parameterized equation for the sphere is ##\vec{r}=\langle a\sin{\theta}\cos{\phi}, a\sin{\theta}\sin{\phi}a\cos{\theta}\rangle##.
The portion inside the cone is the red area below
Just to be clear about the coordinate system, I am using spherical coordinates defined as follows
Now, the spherical shell has a constant density of ##d(x,y,z)=\frac{M}{4\pi a^2}##.
Let's define ##f(x,y,z)=z\cdot d(x,y,z)##.
Then our calculation of ##z_{cm}## is
$$z_{cm}=\frac{\int\int_S f(x,y,z) dS}{\int\int_S d(x,y,z)dS}$$
$$=\frac{\int\int_S f(\vec{r}(\theta,\phi))\cdot \lVert \frac{d\vec{r}}{d\theta}\times\frac{d\vec{r}}{d\phi} \rVert d\theta d\phi}{\int\int_S d(\vec{r}(\theta,\phi)) \lVert \frac{d\vec{r}}{d\theta}\times\frac{d\vec{r}}{d\phi} \rVert d\theta d\phi}$$
The denominator is
$$\frac{M}{4\pi a^2}\int_0^{2\pi}\int_0^{\alpha/2} a^2\sin{\theta}d\theta d\phi$$
$$=\frac{M(1-\cos{(\alpha/2)}}{2}$$
And the numerator is
$$\frac{M}{4\pi a^2}a^3\int_0^{2\pi}\int_0^{\alpha/2} \sin{\theta}\cos{\theta} d\theta d\phi$$
$$=\frac{Ma\sin^2{(\alpha/2)}}{4}$$
Thus when we put numerator and denominator together we get
$$\frac{\frac{Ma\sin^2{(\alpha/2)}}{4}}{\frac{M(1-\cos{(\alpha/2)}}{2}}$$
$$=\frac{a\sin^2{(\alpha/2)}}{2(1-\cos{(\alpha/2)})}$$
However, it seems that either I have made a mistake or the solutions manual is wrong, because they have the answer
Last edited:
