Centripetal force of a ball swinging

[Zarquad]

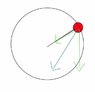
(Look at attached pic) The red ball is attached to a string which is being spun in a vertical circle. The downwards force is gravity and the other green one is the tension force. The blue is the sum of the green vectors. It is the centripetal force because it's the net force (and thus is equal to mv^2/r). On the other hand, isn't centripetal force the "center seeking" force, which means it should be pointed to the center of the circle? In that case, how can it be called the centripetal force?

Thanks.

 

[A.T.]

The downwards force is gravity and the other green one is the tension force. The blue is the sum of the green vectors. It is the centripetal force because it's the net force (and thus is equal to mv^2/r).

No. The tension is the centripetal force equal to mv^2/r. The net force is not purely centripetal in this case, meaning that the speed along the circle varies.

 

[Zarquad]

So does the centripetal force, by definition, ALWAYS point to the center of the circle? Uniform or non uniform circular motion?

e; It still doesn't make sense. The circle is a vertical one (I forgot to mention that) so the amount of tension needed varies. If I wanted to maintain a constant velocity my centripetal force would be constant, but my tension force can't be constant in a vertical circle situation.

 

[A.T.]

So does the centripetal force, by definition, ALWAYS point to the center of the circle? Uniform or non uniform circular motion?

I would say that this the common definition.

The circle is a vertical one (I forgot to mention that) so the amount of tension needed varies.

In that case the centripetal force is tension plus the radial component of gravity. The tangential component of gravity is changing the speed.

 

[Zarquad]

What's the radial component? Gravity is on the y scale, it doesn't have an x component, unless you're changing the axes somehow.

 

[A.T.]

What's the radial component?

Parallel to string.

 

[Zarquad]

So in that case it wouldn't be pointing to the center and my original statement is correct.

 

[Zarquad]

Sorry, I read that as perpendicular for some reason. A gravity component is only parallel to the string twice in the entire circle though.

 

[A.T.]

A gravity component is only parallel to the string twice in the entire circle though.

No. There is always a radial gravity component, exept twice in the circle when it is zero.

 

[Zarquad]

What are you axes/what's your reference?

 

[A.T.]

What are you axes/what's your reference?

It doesn't matter. Parallel to string and perpendicular to string are coordinate independent statements.

 

[Zarquad]

I don't see a component of gravity that is parallel to the string. Can you draw it out?

 

[Doc Al]

I don't see a component of gravity that is parallel to the string. Can you draw it out?

Gravity points downward. Unless the string is horizontal, there will be a component of the weight parallel to the string.

 

[A.T.]

I don't see a component of gravity that is parallel to the string. Can you draw it out?

Just project the weight vector onto the string.

 

[Zarquad]

Oh, alright, I get it now. So in conclusion basically, centripetal force does have to always point to the center?

 

[Doc Al]

So in conclusion basically, centripetal force does have to always point to the center?

Of course. (That's the definition of centripetal.)

 

[Zarquad]

Alright, thanks.