- #1
zinc79
- 9
- 0
I've been having some confusions regarding the centroid coordinates of triangles.
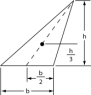
I've been taught that the centroid of a triangle lies at 1/3rd of the perpendicular distance from any selected base to the corresponding top point of the triangle.
I tried to use this shortcut to find the centroid of a triangular shape formed by three uniform-thickness rods, and my answer came out wrong. I consulted my teacher, and he told me that this shortcut applies only to planar triangles of a uniform lamina. The explanation doesn't make sense to me. Why can it not apply? Doesn't every solid object share the same centroid with its hollow counterpart?
What about other variations of the triangle? What if its isoceles, or equilateral? Does the 1/3rd distance rule apply to them or not, then? What about triangles formed with 3 rods, consisting of a circular disc in the middle which touches all three rods ? What if this triangle is equilateral? Does the shortcut apply?
I've been taught that the centroid of a triangle lies at 1/3rd of the perpendicular distance from any selected base to the corresponding top point of the triangle.
I tried to use this shortcut to find the centroid of a triangular shape formed by three uniform-thickness rods, and my answer came out wrong. I consulted my teacher, and he told me that this shortcut applies only to planar triangles of a uniform lamina. The explanation doesn't make sense to me. Why can it not apply? Doesn't every solid object share the same centroid with its hollow counterpart?
What about other variations of the triangle? What if its isoceles, or equilateral? Does the 1/3rd distance rule apply to them or not, then? What about triangles formed with 3 rods, consisting of a circular disc in the middle which touches all three rods ? What if this triangle is equilateral? Does the shortcut apply?