DaTario
- 1,097
- 46
- TL;DR
- How to use Newton's second law to treat differently the two cases below in which a system has its mass increased?
Hi All,
in the figure below we see two cases in which a wheelbarrow moves with speed v, containing a certain mass of water. At a given time t0 a drop of water is added to the system by a dripper. In case 1, the drop enters the system, which increases in mass, having the same speed as the cart. In case 2 the drop is at rest relative to the ground on which the cart moves. Considering Newton's second law expressed in terms of the derivative of linear momentum, how do we treat each case to understand the respective consequences of the increase in mass?
Obs.: consider possible existence of an external and constant force acting on this system.
Best wishes
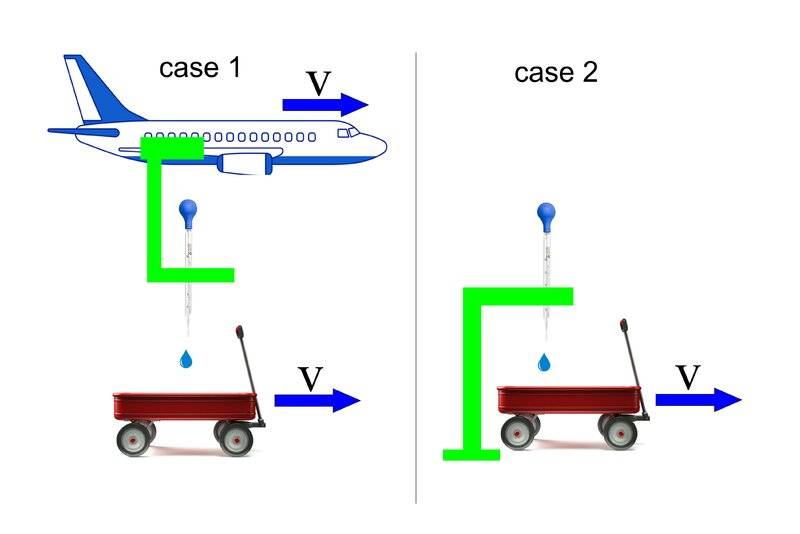
in the figure below we see two cases in which a wheelbarrow moves with speed v, containing a certain mass of water. At a given time t0 a drop of water is added to the system by a dripper. In case 1, the drop enters the system, which increases in mass, having the same speed as the cart. In case 2 the drop is at rest relative to the ground on which the cart moves. Considering Newton's second law expressed in terms of the derivative of linear momentum, how do we treat each case to understand the respective consequences of the increase in mass?
Obs.: consider possible existence of an external and constant force acting on this system.
Best wishes