Change of pressure simple cylinder

[ajd-brown]

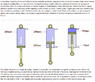
I am trying to calculate the spring rate for an air filled shock-absorber, however I am struggling to get my head around the change non-linearity at the start of compression. Obviously if the shock is fully extended then it will be applying no compressive force to the chassis so that accounts for the force starting from zero. but why does it not increase linearly to begin with? I hasten to add that I understand the non-linearity at the end of the stroke!

Could anybody give me a hint?

Thanks,

 

[haruspex]

Not sure what you mean by initial non-linearity. Any smooth curve starts off effectively linear, but the slope may change.
Which graph are you referring to? The upper graph is for compression against force, and this does nothing surprising. It starts with a low gradient, which gradually increases.
If it's the lower graph, you'll need to explain to me what is meant by "shock travel" in this context.

 

[ajd-brown]

Not sure what you mean by initial non-linearity. Any smooth curve starts off effectively linear, but the slope may change.
Which graph are you referring to? The upper graph is for compression against force, and this does nothing surprising. It starts with a low gradient, which gradually increases.
If it's the lower graph, you'll need to explain to me what is meant by "shock travel" in this context.

Thank you for your reply, I am trying to create the second graph using data I have for a bicycle shock absorber.

Shock travel is essentially the compression of the `air spring'. So at 0 travel, the force is zero because the spring is at its free length (although this is technically not true since there is a greater than atmos. pressure in the shock at this point, (see Pressure Pa. cell in the top left)) and therefore it cannot transmit a force into the frame at this point.

What i am wondering is why will does the bottom graph show a decreasing gradient of force/`air-spring' compression?

I hope this makes sense!

Thanks

 

[haruspex]

Shock travel is essentially the compression of the `air spring'.

So how is that different from compression in the other graph? Is it that these two graphs are from different sources, and it's the difference between them that is puzzling you?

So at 0 travel, the force is zero because the spring is at its free length (although this is technically not true since there is a greater than atmos. pressure in the shock at this point, (see Pressure Pa. cell in the top left)) and therefore it cannot transmit a force into the frame at this point.

Ok, so there is something in the construction which means that the piston cannot go all the way out to the fully uncompressed length. If this something has some elasticity, it could explain the shape of tne lower graph.

 

[ajd-brown]

So how is that different from compression in the other graph? Is it that these two graphs are from different sources, and it's the difference between them that is puzzling you?

It is the same. The lower graph has been created by Fox (a company that sell shocks) and I am trying to achieve the same graph in excel using an ideal gas approximation.

Ok, so there is something in the construction which means that the piston cannot go all the way out to the fully uncompressed length. If this something has some elasticity, it could explain the shape of tne lower graph.

Yes, there is. You are spot on! I hadn't thought of that until now! Essentially there is a secondary smaller volume under the piston which has equal pressure to the volume above and thus at one particular length the resultant force on the piston is zero. which accounts for the force dropping to zero as the travel decreases.

(See image for reference)
http://www.pinkbike.com/news/Tech-Tuesday-negative-spring-air-shocks-2012.html

Thank you for making me think!

 

[OldYat47]

Start with the static load on the shock. That's the simplest way. Then assume that all the heat of compression stays in the air inside the cylinder as the shock is compressed. The internal pressure of the shock at any point of travel is the combination of reduced volume and increased pressure. In most cases the temperature increases quickly enough that no condensation (like water vapor) will occur, and the "fully extended" temperature of the air will be slightly higher than initial temperature due to friction heating.

It is difficult to calculate how hot the air will be over time unless you can model the shock's construction. Remember that it cools some every time the shock extends. Even so, the amount of heat transfer is usually negligible as a component of the pressure. Even friction heating doesn't affect the pressure much (assuming the seals are decently designed).

 

[ajd-brown]

Hi, yes thanks for your input however I have solved the problem and it correlates with experimental results from previous tests. I will post this later on this evening to complete the thread.

I ended up using an polytropic process of Pv^(cv/cp) = C

And by calculating this for both the large and small volumes, assuming that the pressure in both at the equilibrium position was equal, it was possible to get calculate the resultance force on the piston at any point in the travel which yielded the 2nd graph from my 1st post