Changing the minimum value of a probability matrix

[Lucchini]

Homework Statement

I need an idea if it is possible to change the minimum value of a probability matrix, from 0% to a value greater than zero.

Relevant Equations

df['Eventos Anterior'] = df[f'Eventos'].shift(1)

transicoes = df.groupby(['Eventos Anterior', f'Eventos']).size().unstack(fill_value=0)

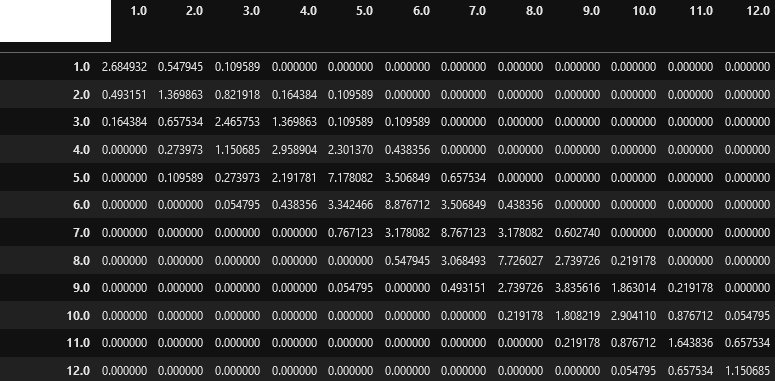
I am doing a study of the possibility of transition between 12 different events. I have a dataframe with these key events (listed from 1 to 12) over a period of time. I constructed a transition probability matrix between these events (photo of the matrix is attached below). As I don't have a very large dataframe, there are some changes that did not occur, for example from event 1 to event 12. How could I change the probability for events that did not occur so that there is a possibility, for example 1%, even if this transition is not present in the dataframe. And so that the rest of the probabilities are adjusted accordingly, maintaining the total probability of 100%.

Is it possible to make such a change? Thank you for your attention!

 

[docnet]

Note: Left stochastic matrices are multiplied on the left by the probability distribution, and the COLUMNS of a transition matrix should sum to 1. What I'm describing here is a right stochastic matrix which has rows sum to 1.

Transition matrices are usually multiplied on the right by the probability distribution, and each row should sum to 1 to ensure the total probability is conserved. The row of your matrix don't sum to 1, and they sum to different numbers. Would it make sense to multiply each row by a normalizing constant? (I'm asking because I don't know how you derived the matrix). I assume that your dilemma can be solved by having the correct transition matrix. But if you still want to change the zero entries, make them very small to ensure that the model is was accurate as possible.

 

[FactChecker]

Transition matrices are usually multiplied on the right by the probability distribution, and each row should sum to 1 to ensure the total probability is conserved. The row of your matrix don't sum to 1, and they sum to different numbers. Would it make sense to multiply each row by a normalizing constant? (I'm asking because I don't know how you derived the matrix). I assume that your dilemma can be solved by having the correct transition matrix. But if you still want to change the zero entries, make them very small to ensure that the model is was accurate as possible.

CORRECTION: In the answer below, it is the COLUMNS that should add up to 1, not the rows. The i-row elements, $r_{i,j}$, simply add up tho the proportion of the initial states that will transition to state i.

Good catch. Any row, $r_i = (p_{i,j})$, of the transition matrix should be the probabilities of transitions from state i to state j in one transition. So the row must be a probability distribution and sum to 1. That can be multiplied on the right by the initial distribution of states. The results of the multiplication is the distribution of states after one transition.
IMO, the first step is to correct the rows to probabilities. There might be a computation error or normalization might be needed.
The OP sounds like there is a prior belief in the transition probabilities that does not agree with the sample used to generate this (not a transition) matrix. This sounds like a good exercise in Bayesian theory. The question would be how the prior belief distributions in each row of the transition matrix should be adjusted by the sample results. I would like to see what @fresh_42 or @Dale advise on this. I think they are experts in Bayesian techniques.

 

[Dale]

Indeed, as @FactChecker mentioned, this would naturally happen in a Bayesian analysis. If you have a uniform prior or some other prior that includes the non-sampled transitions, then they will remain non-zero after.

 

[docnet]

CORRECTION: In the answer below, it is the COLUMNS that should add up to 1, not the rows. The i-row elements, $r_{i,j}$, simply add up tho the proportion of the initial states that will transition to state i.

You're right, it's probably a left stochastic matrix! It seems to be the most often used, more than the right stochastic one.