Charges of capacitors in series and in parallel

[greg_rack]

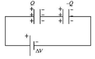
Very simply, I can't understand why the charges of capacitors placed in series are all the same, and why even the total one(of the circuit) is equal to those.
How is it possible that the total charge is the same as the individual ones?
There must be some concept/property about capacitors which I'm not getting.
On the other hand, for parallel capacitors, the total charge is the sum of those of the single capacitors, and that's what I would assume generally and logically.

 

[Doc Al]

Consider the wire connecting the two capacitors. Assuming it was not given some additional charge, the sum of the charges on the two connected plates must be zero.

 

[greg_rack]

Consider the wire connecting the two capacitors. Assuming it was not given some additional charge, the sum of the charges on the two connected plates must be zero.

Why? Couldn't they just bring the potential to zero by having the sum of $\frac{q}{C}$ ratios equal to the battery voltage??

 

[Doc Al]

Why?

Because charge is conserved. They start with zero charge and that just gets distributed between the connected plates.

Couldn't they just bring the potential to zero by having the sum of $\frac{q}{C}$ ratios equal to the battery voltage??

Not sure what you are saying here. The battery voltage equals the sum of the voltages across each capacitor.

 

[Delta2]

You should consider the total charge that moves to charge the capacitors.
In the series case the total charge that moves is $Q=Q_1=Q_2$ because first it moves through one capacitor and then the same(because they are in series) charge it moves through the second capacitor.
In the parallel case $Q_1$ charge moves through one branch and $Q_2$ charge moves through the other branch so the total charge that moves is $Q=Q_1+Q_2$.

 

[kuruman]

Another way of saying the same thing is this. Consider the "H" shaped conducting piece between the two capacitors. It is initially neutral and, because it is isolated from the battery, it remains neutral when the battery is hooked up. Thus the total negative charge on the left side of the H must be equal in magnitude to total positive charge on the right side. Since, by definition, the charge $Q$ on a capacitor is the absolute value on either one of its plates, the two capacitors must have the same charge. Note that no mention was made of the capacitance of each capacitor, therefore this result is true regardless of the capacitances; it's a result of charge conservation.

 

[Dale]

Yet another way of saying the same thing is to remember that the charge on a capacitor is given by $q(t) = \int i(t) \ dt$. Since the capacitors are in series $i(t)$ is the same for all of them so $q(t)$ is also the same for all of them.

Simply put, charge conservation and the fact that charge does not cross the capacitor lead to this result.

 

[greg_rack]

Thanks guys, I got it!