Charging a capacitor, time constant stuff

[Linus Pauling]

1. The switch in the figure has been closed for a very long time.

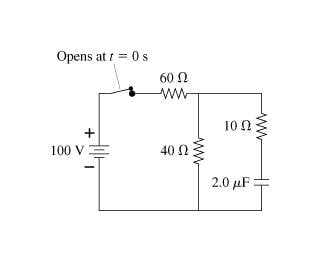
A.) What is the charge on the capacitor?
B.) The switch is opened at t = 0s. At what time has the charge on the capacitor decreased to 12% of its initial value?



2. Q=VC, tau= RC, etc.



3. A.) The capacitor will have a potential equal to Vbat = 100V. Q = VC = (100V)(2*10^-6 F) = 2*10^-4 C = 0.20 uC

b.) e^-x = e^-(t/tau)
2.12*tau = t
2.12RC = t
2.12*70ohm*(2*10^-6F) = t = 30ms

 

[vela]

3. A.) The capacitor will have a potential equal to Vbat = 100V. Q = VC = (100V)(2*10^-6 F) = 2*10^-4 C = 0.20 uC

That should be 20 μC.

b.) e^-x = e^-(t/tau)

What is x?

2.12*tau = t
2.12RC = t
2.12*70 ohms*(2*10^-6 F) = t = 30 ms[/b]

You used the wrong value for R.

 

[phyzguy]

I think you're missing something. When the switch has been closed for a long time, there will be no current through the 10 ohm resistor. However, there WILL be current through the 60 ohm and 40 ohm resistors. So the capacitor does not charge all the way to 100 V, but to an intermediate value determined by the resistive divider of the 40 ohm and 60 ohm resistors.

 

[Linus Pauling]

That should be 20 μC.

That is incorrect...

What is x?

You used the wrong value for R.

I just set e^x = e^(t/tau) and solved for t. I actually solved this problem before (the answer is 0.21 ms) but and made the same mistake (getting 0.30 ms) before getting it right... but I don't remember how I did it...

 

[Linus Pauling]

I think you're missing something. When the switch has been closed for a long time, there will be no current through the 10 ohm resistor. However, there WILL be current through the 60 ohm and 40 ohm resistors. So the capacitor does not charge all the way to 100 V, but to an intermediate value determined by the resistive divider of the 40 ohm and 60 ohm resistors.

Actually, this made me remember how I got the correct time value. I remember saying that once the capacitor is fully charged, current would just go through that inner loop around and around, so the 40 and 10ohm resistors in series gives 50ohm*2.12.*capacitance = 0.21 ms... but I don't think I fully understand this conceptually.

Also, what do you mean by "resistive divider"? And why doesn't the capacitor charge to 100V? I understand why there'd be no current through the 10ohm resistor - the capacitor is fully charged and so there's no current by the loop law... but why isn't charged to V_bat?

Thanks.

 

[vela]

That is incorrect...

As phyzguy pointed out, the number you calculated itself was wrong, which I didn't notice, but my point was you converted the units incorrectly: 20x10^-4 C isn't 0.20 uC; 0.20 uC = 0.20x10^-6 C = 2x10^-7 C.

I just set e^x = e^(t/tau) and solved for t. I actually solved this problem before (the answer is 0.21 ms) but and made the same mistake (getting 0.30 ms) before getting it right... but I don't remember how I did it...

But what is x? It's just some variable that mysteriously appears with no indication of what it stands for, then the number 2.12 just appears.

 

[Linus Pauling]

As phyzguy pointed out, the number you calculated itself was wrong, which I didn't notice, but my point was you converted the units incorrectly: 20x10^-4 C isn't 0.20 uC; 0.20 uC = 0.20x10^-6 C = 2x10^-7 C.

I don't understand. Q = VC, but V is not 100V. I don't understand why not.

But what is x? It's just some variable that mysteriously appears with no indication of what it stands for, then the number 2.12 just appears.

Honestly I don't know. I figured out the answer as 0.21ms earlier in the week and I'm pretty sure I used the 2.12 value... but I don't remember why I had that x...

 

[vela]

I don't understand. Q = VC, but V is not 100V. I don't understand why not.

Perhaps a better question is, why would it be? Just because there's a 100-V battery in the circuit doesn't mean all the elements individually have a 100-V drop across them.

 

[ideasrule]

I don't understand. Q = VC, but V is not 100V. I don't understand why not.

It IS 100V. 2 uF * 100 V = 200 uC, not 0.2 uC.

Honestly I don't know. I figured out the answer as 0.21ms earlier in the week and I'm pretty sure I used the 2.12 value... but I don't remember why I had that x...

OK, work it out from first principles. First, what's R? That is, what is the equivalent resistance of all the resistors? Second, Q=Q0*e^(-t/RC), and you want to find the point where Q=0.12Q0. Just plug that in and solve the resulting equation.

 

[ideasrule]

I think you're missing something. When the switch has been closed for a long time, there will be no current through the 10 ohm resistor. However, there WILL be current through the 60 ohm and 40 ohm resistors. So the capacitor does not charge all the way to 100 V, but to an intermediate value determined by the resistive divider of the 40 ohm and 60 ohm resistors.

That's not correct. There's no current through the 10 ohm resistor and the potential difference across the right branch is 100V, since the branch straddles the battery. No current means no voltage drop across the resistor, so all the voltage drop must be across the capacitor.

 

[vela]

That's not correct. There's no current through the 10 ohm resistor and the potential difference across the right branch is 100V, since the branch straddles the battery. No current means no voltage drop across the resistor, so all the voltage drop must be across the capacitor.

No, phyzguy is right. There's no current through the 10-ohm resistor, but there is current running through the left loop. The voltage across the right branch is just the voltage across the 40-ohm resistor, not the entire 100 volts from the battery.

 

[ideasrule]

No, phyzguy is right. There's no current through the 10-ohm resistor, but there is current running through the left loop. The voltage across the right branch is just the voltage across the 40-ohm resistor, not the entire 100 volts from the battery.

Oh, I thought the 60-ohm resistor was in parallel with the 40-ohm resistor. My bad, phyzguy is right.

 

[Linus Pauling]

Ok, I'm still a bit lost. First, in case anyone has said the answer is 200uC, it's not.

Ok, so the voltage drop on the capacitor must be the same as that for the 40ohm resistor that's in parallel to it. What is that voltage drop? Is this the calculation for it:

Inverse of (1/40) + (1/10) = 8 ohm + 60 ohm = 68 ohm.
Equivalent I = V/R = 100V/68ohm = 1.47A

For 40 ohm resistor, V = 1.47A*40ohm = 58.8V?

 

[phyzguy]

Still not right. When the switch has been closed for a long time, current is only flowing through the 40 ohm and 60 ohm resistors, which are in SERIES. So add them up to get the total resistance, and divide V by the total resistance to get the current. This current is then multiplied by the 40 ohm resistor to ge the voltage drop across the 40 ohm resistor, which is what the capacitor charges up to. When you've done this calculation, I think you'll see why it's called a voltage divider.