SUMMARY
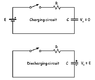
The current-time graph for both charging and discharging capacitors exhibits similar exponential behavior due to the relationship between potential difference (p.d.) and current. During charging, the p.d. across the capacitor increases, causing the current to decrease as the capacitor approaches the battery's p.d. Conversely, during discharging, the initial p.d. across the capacitor is maximum, and as the charge leaves, the p.d. and current decrease exponentially. This behavior is governed by Ohm's Law (I = ΔV/R) and Kirchhoff's Voltage Law (KVL).
PREREQUISITES
- Understanding of capacitor charging and discharging principles
- Familiarity with Ohm's Law (I = ΔV/R)
- Knowledge of Kirchhoff's Voltage Law (KVL)
- Basic circuit analysis skills
NEXT STEPS
- Study the mathematical derivation of capacitor charging and discharging equations
- Learn about the impact of resistance on capacitor discharge rates
- Explore practical applications of capacitors in RC circuits
- Investigate the effects of different resistor values on current flow in charging and discharging scenarios
USEFUL FOR
Students studying electrical engineering, physics enthusiasts, and anyone interested in understanding capacitor behavior in circuits.