Charging and discharging capacitors - current time graph

[jsmith613]

Homework Statement

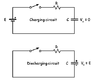
why is the current-time graph for a charging AND discharging capacitor the same?

Homework Equations

The Attempt at a Solution

Q=It
so for a discharging capacitor as time goes on the charge stored decreases so current decreases

BUT for a charging capacitor charge increases so current should increase??

 

[gneill]

Think in terms of the potential difference that is driving the current. How much of the potential appears across the resistor over time?

 

[jsmith613]

Think in terms of the potential difference that is driving the current. How much of the potential appears across the resistor over time?

well p.d increases over time

 

[gneill]

well p.d increases over time

In both cases? For the resistor?

 

[jsmith613]

I think so...

 

[gneill]

Sketch the PD across the capacitor for the charging case. You should be able to infer the PD across the resistor using KVL for the circuit (battery, resistor, capacitor). What do you find?

 

[jsmith613]

Sketch the PD across the capacitor for the charging case. You should be able to infer the PD across the resistor using KVL for the circuit (battery, resistor, capacitor). What do you find?

well in one case it is increase (charging) and the second case it is decreasing (discharging) expotentially

 

[gneill]

well in one case it is increase (charging) and the second case it is decreasing (discharging) expotentially

To what are you referring by 'it'? Let us be clear; there are three potential differences to be concerned with in the circuit. One is the PD of the battery which is fixed (a constant), the second is the PD across the resistor, and the third is the PD across the capacitor.

 

[jsmith613]

To what are you referring by 'it'? Let us be clear; there are three potential differences to be concerned with in the circuit. One is the PD of the battery which is fixed (a constant), the second is the PD across the resistor, and the third is the PD across the capacitor.

in charging case, pd across capacitor increases and in discharging case pd across capacitor decreases

no idea about resistor, sorry :(

 

[gneill]

in charging case, pd across capacitor increases and in discharging case pd across capacitor decreases

no idea about resistor, sorry :(

How do the potential differences around the loop add up?

 

[jsmith613]

V = V₁ + V₂

so I would presume the emf across the resistor falls as p.d across capacitor increases (and then increases as p.d across capacitor decreases)

 

[gneill]

V = V₁ + V₂

so I would presume the emf across the resistor falls as p.d across capacitor increases (and then increases as p.d across capacitor decreases)

That's nearly right. Certainly the p.d. across the resistor falls as the p.d. across the capacitor rises when it's charging. But what about the case where the capacitor is discharging? In that case the battery is removed and replaced with a piece of wire (the circuit is different). The capacitor starts out with some initial p.d. across it, and the resistor is connected directly across the capacitor. So the resistor starts with the same p.d. as the capacitor...

 

[jsmith613]

That's nearly right. Certainly the p.d. across the resistor falls as the p.d. across the capacitor rises when it's charging. But what about the case where the capacitor is discharging? In that case the battery is removed and replaced with a piece of wire (the circuit is different). The capacitor starts out with some initial p.d. across it, and the resistor is connected directly across the capacitor. So the resistor starts with the same p.d. as the capacitor...

hold on...when its charging the resistor is not involved
it is only involved during discharging

surely your approach is wrong?

 

[gneill]

hold on...when its charging the resistor is not involved
it is only involved during discharging

surely your approach is wrong?

The resistor must be there in both cases. Otherwise you've got an unrealistic circuit.

 

[gneill]

 

[jsmith613]

The resistor must be there in both cases. Otherwise you've got an unrealistic circuit.

well I am used to using a two way switch :S

 

[gneill]

well I am used to using a two way switch :S

Does that change the essential functionality of the two scenarios?

 

[jsmith613]

Does that change the essential functionality of the two scenarios?

well no but it does change the circuit diagram

 

[gneill]

well no but it does change the circuit diagram

Equivalent circuits are a powerful analysis tool. If you're worried about esthetics, post the original circuit diagram and we can work from that

 

[jsmith613]

Equivalent circuits are a powerful analysis tool. If you're worried about esthetics, post the original circuit diagram and we can work from that

see diagram!

 

[gneill]

see diagram!

The circuit in the diagram has a small problem: There's no resistance in the path when the switch is in the 'charging' position. For ideal components that would mean that the battery would "see" no resistance between its own p.d. and the current p.d. of the capacitor, which begins at zero volts. The ideal battery would supply an infinite current to bring the capacitor p.d. up to that of the battery instantaneously. No gradual increase or decrease in current in that case, just BANG! You're done!

In real life there is always resistance in the path, even if it's just the resistance of the wiring. A small modification to your circuit will fix this. Two choices: Either move the resistor so that it will be in either current path, or add a second resistor to represent the resistance in the charging path:

For both versions, when the switch is moved to the left to charge the capacitor, the resulting circuit is the same as the Charging Circuit that I posted earlier. Similarly, the circuit that results when the switch is moved to the right is the same as the Discharging Circuit in that post.

In any circuit, current is moved by a potential difference. The greater the potential difference the greater the current for a given resistance in between. This is just Ohm's Law: I = ΔV/R.

What you need to do is spot the initial potential difference that each circuit begins with (which devices in the circuits are holding a potential before the path is closed?). That sets the initial current. Then determine how that potential difference changes over time as the current flows.

 

[jsmith613]

---

ok so is this what your saying:

Initially there is a greater potential difference between the resistor, power source and capacitor.

When charging the p.d decreases so the flow of charge (the current decreses)

when the circuit discharges the potential difference between the resistor and capacitor is maximum at the start. As charge leaves the capacitor the p.d falls and therefore so does the current?

 

[gneill]

ok so is this what your saying:

Initially there is a greater potential difference between the resistor, power source and capacitor.

When charging the p.d decreases so the flow of charge (the current decreses)

when the circuit discharges the potential difference between the resistor and capacitor is maximum at the start. As charge leaves the capacitor the p.d falls and therefore so does the current?

Yup. That's it

 

[jsmith613]

Yup. That's it

yey
thanks for this