Circle tangent to two lines and another circle

[Anachronist]

TL;DR

Find center of a circle tangent to perpendicular lines x=a and y=b, and also tangent to a circle of radius r at the origin.

I'm trying to solve this for a model I'm making in OpenSCAD.

Given a circle of radius r centered on the origin, and two perpendicular lines at x=a and y=b, where is the center (x1,y1) of a circle that is tangent to both lines and the centered circle?

Here's a picture:

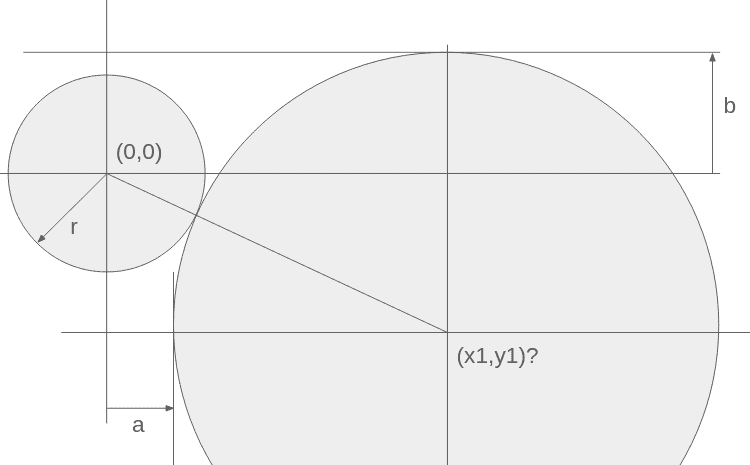
I thought it would be easy, like solving for a circle that intersects 3 points, but there's something I'm not getting here. It's been 4 decades since I had to solve problems like this.

I know that the distance between (0,0) and (x1,y1) should be the sum of the two radii. I could solve it iteratively, but it feels like there should be a closed-form solution here.

 

[Hill]

You have three unknowns, $x_1, y_1, r_1$ and three equations from the three tangent conditions. You will need to solve a quadratic equation.

 

[Anachronist]

Thanks, I believe I figured it out.

From the diagram, I have

$x_1^2+y_1^2 = (r+R)^2$

where $R$ is the radius of the unknown circle. I also know that $x_1=a+R$ and $y_1=b-R$. That means

$(a+R)^2 + (b-R)^2=(r+R)^2$

and I have a quadratic expression with one unknown, $R$. That can be solved by the quadratic equation, and I get this:

$R=b-a+r \pm \sqrt{2}\sqrt{(r-a)(b+r)}$

With that I can solve for $(x_1,y_1)$.