Circuit Transformations: Norton's Theorem

[Master1022]

Homework Statement

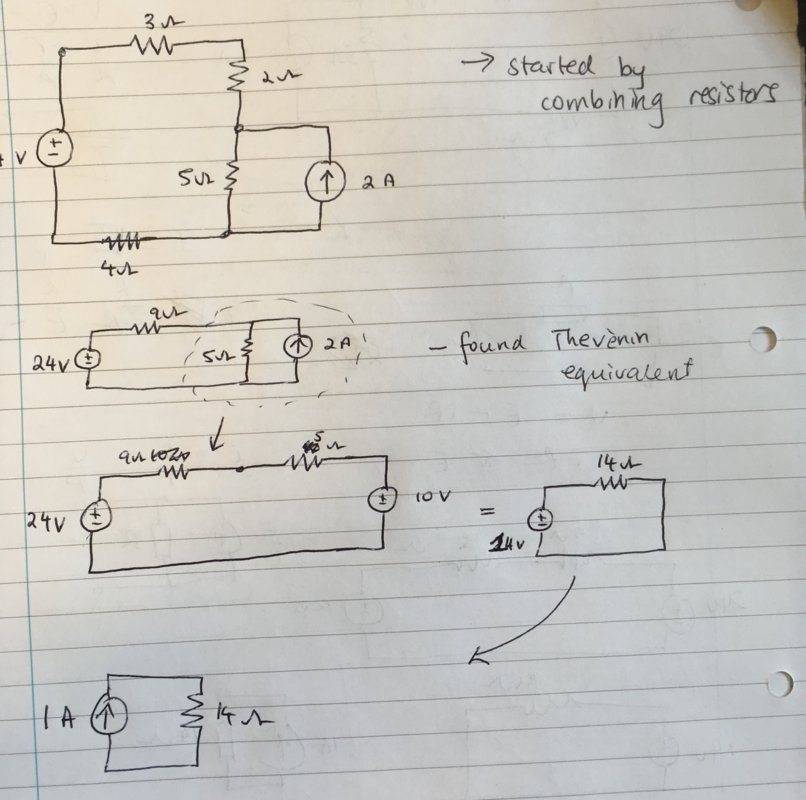
Convert the circuit into an equivalent resistance and a current source.

Relevant Equations

$V = E - IR$

Picture of the circuit is posted below. Apologies, the voltage source on the left should read 24 V. My question is: What is wrong with this method? [Edit: Sorry if it wasn't clear- the method in the picture yields the wrong answer]

When I originally did the question, I just turned the LHS into its Norton equivalent and then combined to get the answer. However, why can't it be done this way as well (i.e. convert RHS to Thevenin equivalent, and then continue).

My initial thoughts have been to do with that we cannot combine the Thevenin equivalent in that way, but I was wondering why that would be the case?

 

[DaveE]

It looks good to me. I'm not 100% sure I understand your question.
The point of Norton/Thevenin equivalent transformations is that they are equivalent. So you can apply them in any order that makes simplification of the attached network easy. When there are multiple sources in the circuit then there will be different approaches to the simplification based on which source you choose to transform at each step. In a very general sense the process is transform a section, then add resistors to simplify, then repeat until the network is reduced to it's simplest form.
I've never really understood why 2 guys (Norton and Thevenin) both get credit for what I see as one equivalence transformation. I think it confuses students to refer to them as separate things.

 

[Master1022]

It looks good to me. I'm not 100% sure I understand your question.
The point of Norton/Thevenin equivalent transformations is that they are equivalent. So you can apply them in any order that makes simplification of the attached network easy. When there are multiple sources in the circuit then there will be different approaches to the simplification based on which source you choose to transform at each step. In a very general sense the process is transform a section, then add resistors to simplify, then repeat until the network is reduced to it's simplest form.
I've never really understood why 2 guys (Norton and Thevenin) both get credit for what I see as one equivalence transformation. I think it confuses students to refer to them as separate things.

Sorry, I should have made it clearer. Doing this alternative method yields the wrong answer, whereas the other method gives the 'correct' answer.

 

[DaveE]

You changed the problem at the last step when you combined 9+5 ohms into 14 ohms. The point of these transformations is to simplify a 1 port network, so you need to identify up front what you connection points are. For example, across the 5 ohm resistor. As you apply the transforms it is easy to loose sight of the fact that you may be changing loops and nodes in the process.

 

[Master1022]

You changed the problem at the last step when you combined 9+5 ohms into 14 ohms. The point of these transformations is to simplify a 1 port network, so you need to identify up front what you connection points are. For example, across the 5 ohm resistor. As you apply the transforms it is easy to loose sight of the fact that you may be changing loops and nodes in the process.

Thank you for your response. So I cannot usually combine things across the 'central' node unless they are in parallel?

 

[DaveE]

Thank you for your response. So I cannot usually combine things across the 'central' node unless they are in parallel?

Yes, that's correct. It may help to draw into your schematic the measuring device for the parameter you are interested in. Like a voltmeter between nodes, or an ammeter around a branch. Then you can more easily see what can or can't be changed without altering the measurement