jgray
- 10
- 0
Homework Statement
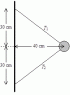
A 0.60 kg sphere rotates around a vertical shaft supported by two strings, as shown. If the tension in the upper string is 18 N. Calculate
the tension in the lower string?
the rotation rate (in rev/min) of the system?
Homework Equations
v=2(pi)r/T
Fr= mv^2/r
ω = v/R
The Attempt at a Solution
I believe I have the first part correct, my question is really about the second part. For the second part of the question: I calculated the x components of each tension force to find the centripetal force = 20.96N. I then found the velocity by rearranging the equation: Fr = mv^2/r to get 3.74m/s. I used the equation ω = v/R to get 9.35 rads/sec and converted it to 89.3 rpm by multiplying 9.35 by 60s and dividing it by 2(pi). Am I on the right track?? Just seems like a small answer…