Circulation of water in a cylindrical reservoir

[RiotRick]

Homework Statement

One important quantity to characterise a fluid is the circulation. Given $\Gamma$ a closed oriented path inside the fluid, the circulation $C_r$ along the path $\Gamma$ is the integral $C_r =\oint{\vec{v}*\vec{dl}}$


a) Consider a cylindrical reservoir of radius r containing a fluid rotating with constant angular velocity $\omega$. What is the circulation $C_r$ with path defined as in figure 1?

b) Now, let us consider the case in which the velocity is not constant but rather the circulation, around any circle of radius r centred at the axis, is constant (independent of r). What is the velocity as a function of r in this case? ( it's 1:1 written like that. I guess they mean omega is not constant but the velocity is constant )

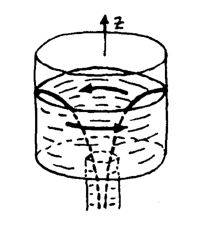
c) A practical application for the case of constant circulation is a drain in a sink. Using Bernoulli’s equation and considering p = p0, the atmospheric pressure, what is the fluid height z in figure 2 as a function of r? Consider Bernoulli’s equation a constant everywhere

Relevant Equations

I honestly don't know

Fig1:

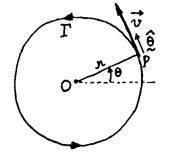
Fig2:

We haven't covered this topic yet, but they expect us to solve it and I'm not 100% sure what I'm doing.

a) $C_r =\oint{\vec{v}*\vec{dl}} = \int{\omega*r*dl} = \omega*\int{r*r*d\phi} = \omega*r^2*2pi$

b) Now here I begin to struggle. If v is constant, can I simply pull it out of the integral? But it still depends on omega right? During my web research I've also seen the circulation problem explained with coulomb but that's one thing I'm not into yet. Can I simply think of a water molecule with mass m being pulled by the centripetalforce?

 

[RiotRick]

Ok I've found the solution on the caltech website. It's public and open, so I guess I can link it here: http://www.feynmanlectures.caltech.edu/II_40.html

it's 40-4. But how can I obtain the Formula $h`=\omega^2*r^2/2g$