Clarification about Mutual Inductance

[Physicslearner500039]

Homework Statement

In if coil 2 is turned so that its axis is vertical, does the mutual inductance increase or decrease? Explain.

Relevant Equations

emf = $\frac {-N_{2} {d\phi}_{B2}} {dt}$ $M_{21} = \frac {{N_2}{\phi}_{B2}} {i_1}$

emf = $\frac {-N_{2} {d\phi}_{B2}} {dt}$ $M_{21} = \frac {{N_2}{\phi}_{B2}} {i_1}$ are the equations

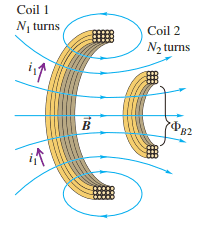
This is the original position, now the coil 2 is moved so the axis is perpendicular. The flux ${\phi}_{B2}$ due to i1 is the amount of flux cutting the coil 2 due to change in current i1. My answer is 0, since no flux cuts the Coil 2 in 90 degrees position. Is it correct? My main confusion is with respect to the area of the coil. How to consider it? i do not see the coil 2 as closed circuit it is open loop. So, what will be the area. Please advise.

Note: One another problem is i cannot preview the Homework statement and the Relevant Equations section. I have a workaround for the equations section, but still not sure if latex symbols work for the Homework statement. Please advise.

 

[Steve4Physics]

My answer is 0, since no flux cuts the Coil 2 in 90 degrees position. Is it correct?

Hi. You are correct. There is (almost) zero flux through rotated coil-2. I say 'almost' because the coil has finite thickness and is spiral-wound which means a *very* small amount of flux cuts the coil - we can usually treat it as zero.

My main confusion is with respect to the area of the coil. How to consider it? i do not see the coil 2 as closed circuit it is open loop. So, what will be the area.

I'm not sure I understand the question. But see if this helps.

Visualise the flux and area as you have done here. You can then 'see' if flux passes through the coil, rather than being parallel to the coil's plane.

Mathematically, you multiply the *component* of flux perpendicular to the area (i.e. parallel to the area's normal) by the area.

For example, for area A with its normal at angle θ to uniform field B, the flux through the area is Φ = ABcosθ (which is zero if θ = 90º).

not sure if latex symbols work for the Homework statement.

Sorry, can't help with that.

 

[Physicslearner500039]

When rotated 90 Degrees

Is my understanding correct? Please advise.

 

[TSny]

My main confusion is with respect to the area of the coil. How to consider it? i do not see the coil 2 as closed circuit it is open loop. So, what will be the area.

I'm not sure, but I'm wondering if the figure is misleading you. The figure does not show the entire coils. The figure is a "cutaway" figure. The coils are complete circular coils.

 

[Steve4Physics]

I agree with TSNy (#4). The coils are meant to be omplete circular ones (or they cannot be called 'coils'!). The diagram is simply a cut-away schematic.

If they were actual open half-coils as shown, there could be no current through either and the question wouldn't make sense.

 

[rude man]

I interpret this as 2 neighboring coils with axes parallel, then one is rotated 90 deg. so that now the axes are mutually perpendicular.

In which case, what is mutual inductance in terms of the two coils' fluxes?