Clarifying Notation

[sponsoredwalk]

This post is an example of the danger of confusing notation, no need to read on!

I was confusing Bourbaki notation with set notation and mixing them
together in a really messy way, drove me crazy!


The basic problem is that I want to be extremely clear about the sets that
mathematical manipulations and operations are taking place in, I am hoping for
someone who really understands this to read what I've written closely and point
out what is getting me all mixed up, though of course reading &/or responding
isn't mandatory :tongue2: - but it is a long post even though it's dealing with just
one idea :yuck:

The set-theoretic definition of a function is f = (X,Y,F) where F is a subset of
ordered pairs of the Cartesian product of X & Y, (i.e. F ⊆ (X x Y) a relation).
I copied this out of Bourbaki's set theory.

But isn't a function itself a relation and therefore musn't we write (X,Y,f) as the set
in which the function acts? To expand this out (X,Y,f) = (X,Y,(X,Y,F)).
I've come across notation that specifies (X,Y,f) as ((X,Y),f).
http://www.math.bilgi.edu.tr/courses/Lecture%20Notes/SetTheoryLectureNotes.pdf [Broken]
So ((X,Y),f) = ((X,Y),((X,Y),F)) would seem to make sense.

Bourbaki calls f a set & F it's graph but the notation in the .pdf file says that f
would be defined in the way I've explained above, i.e. that F is a subset of XxY.
The thing is that since a function f is itself a relation shouldn't it be a relation
in a set itself, i.e. ((X,Y),f)?

Assuming that the above is the way to think about these things, how would I think
of both F & f? In f = (X,Y,F), F ⊆ (X x Y) so (x,y) ∈ F or xFy.

How about f? I think f ⊆ (X x Y) so (x,y) ∈ f or xfy.

I don't understand how this makes sense because in the set f = (X,Y,F) Bourbaki
writes f : X → Y so for (X,Y,f) I'd have to set g = (X,Y,f) and write g : X → Y.

The problem of being extremely clear about what sets you are using is particularly
interesting when doing linear algebra.

The use of set-theoretic notation in linear algebra both clarifies things for me and
brings up similar questions, for a vector space V I could write ((V,+),(F,+',°),•)
with the clarification that:

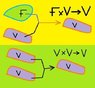
in (V,+) we have + : V × V → V,

in (F,+',.) we have (+' : F × F → F) & ( ° : F × F → F).

In • we have (• : F × V → V) or perhaps [• : (V,+) × (F,+',°) → (V,+)]?

This notation clearly illustrates why the two operations, vector addition and
scalar multiplication are used on a vector space and the axioms for each clearly
jump out, i.e. (V,+) is abelian, (F,+',°) is a field and • isn't the clearest to me but
I think it's similar to the way that + & ° are related in a field, i.e. "multiplication
distributes over addition".

Relating all of this to the concerns I had above in a clear manner, in the set (F,+',°)
it would make sense that +' is a set of the form (F,+'') where +'' is a subset of the
cartesian product of F x F. Similarly with °, and in the set (V,+) you'd have
something similar, also in • you'd have a crazy set ((V,+), (F,+',°), •') or including
even more brackets (((V,+), (F,+',°)), •')

There is another problem when you want to give a vector space a norm, would I
write ((V,+),(F,+',°),•,⊗) where ⊗ : V x V → F ? Would ⊗ itself suggest the subset
((V,+), (F,+',°), ⊗') in the manner explained above? I don't think so because ⊗'
would be the set of ordered pairs (x,a) with x ∈ V and a ∈ F but since V x V → F
you've got the map (x,x') ↦ a, quite confusing tbh and need help with this.

All this seems crazy but it also makes a lot of sense, I want to be very rigorous
about what I'm doing and all of the above seems to suggest itself but it could be
a lot of nonsense caused by simple confusion of a particular issue in the post ,
I'm thinking that (X,Y,F) implying (X,Y,f) is the culprit but again this idea clarifies things.
If you read to this point thanks so much , thanks for taking the time

 

[AlephZero]

Don't confuse rigor with pedantry.

There is no sense complicating the notation to the extent where it becomes unreadable and unwriteable. If you are working in a context where a function could not possibly be of anything else but X and Y, you don't really need to spell out that fact on every line of the argument.

 

[disregardthat]

To the contrary Aleph, I think it's healthy to have these fundamental things clear as day before you even though you would never use this detailed formalism in an argument.

I don't see the problem with the function definition. If you define a function f as a tuple (X,Y,F), X domain, Y co-domain and F graph, what is the ambiguity? Why would you want to write f = (X,Y,f) ? A function is not (set theoretically) equal to it's graph in this definition. You could alternatively define a function as a graph, you'd have the domain baked into this (union of first-coordinates), but the co-domain would be left undefined. You could however define the co-domain as the union of the second-coordinates (range), but that isn't common.

In • we have (• : F × V → V) or perhaps [• : (V,+) × (F,+',°) → (V,+)]?

• is a binary relation on V x F, not (V,+) x (F,+',°). Consider the following absurdity in the latter case: assuming the usual set-theoretical definition of tuples, {V} ∈ (V,+) and {F} ∈ (F,+',°), so what is •({V},{F})?

Commutativity, distributivity and such are properties that can all be expressed purely in terms of the functions themselves. E.g. a(b+c) = ab+bc for a ring with + and * is just *(a,+(b,c))=+(*(a,b),*(b,c)) for all elements a,b,c in the ring.

 

[sponsoredwalk]

Well as I currently understand it Bourbaki uses this idea of (X,Y,F) where F is the graph.
However a lot of contemporary set theory would define the set (X,Y,F) where F is a subset
of the cartesian product of ordered pairs. This is apparently a relation that picks specific
ordered pairs from X x Y. Now, I've been told just last night that a function is not
always a relation whereas I'd previously read that a function is just a special type of
relation so I am mightily confused - sometimes it is a function and other times its just a
relation that satisfies these functions. You see I was confusing Bourbaki notation with other
notations, functions and relations etc... and I don't really understand the difference
between this Bourbaki graph and the convention of a set of ordered pairs, I am going to put
all of this down to a case of not understanding the various uses of notation and am going to
read a few books and be very conscious of the differences.

As for the set [• : (V,+) × (F,+',°) → (V,+)] yeah you're absolutely right & I thought up
the set (V,F,((V,V),+),((F,F),+'),((F,F),°),•) which I think would satisfy that requirement,
it seems to me that this huge set can satisfy everything I wrote about vector spaces
above, what do you think? As far as I see this set, • is a subset of V x F and this
big set also accounts for operations like F x F etc... but I can't help thinking of
F x F and V x F as different sets. If you read this physicsforums thread post you'll see
that I'm not the only one who is thinking along these lines.

I just get the feeling that we are creating millions of sets everytime we do something in
mathematics, for instance I've seen pictures of V x V → V where there are three sets in
the picture. More explicitly V x V' → V'' where an arrow comes out of V, an arrow out of V'
and they join up and land in the V'' set, there's 3 of the same sets already so I honestly
don't know if I just think of one set or three. This is further compounded when thinking of a
group, (G,°), isn't °:G x G → G ? Is (G,°) really (G,G,°) or more explicitly ((G,G),°)?

Apologies if that sounds stupid but I have to say it, it's most likely wrong but I just have
to get it out.

 

[disregardthat]

The graph of a function is by definition a subset of the cartesian product of domain and co-domain with unique first-coordinates, if that's causing the confusion. A (EDIT:) function is a binary relation between the domain and co-domain.

As for the set [• : (V,+) × (F,+',°) → (V,+)] yeah you're absolutely right & I thought up
the set (V,F,((V,V),+),((F,F),+'),((F,F),°),•) which I think would satisfy that requirement,
it seems to me that this huge set can satisfy everything I wrote about vector spaces
above, what do you think?

I don't understand you entirely, but remember that a function (also •,+ etc..) is always on the form (X,Y,F), where X is the domain. So if you are defining a function on, say, a group (G,*), the domain is just the set of elements G, not the set-theoretic definition of a group (the tuple (G,*)). I.e. X = G, X $$\not =$$ (G,*).

As far as I see this set, • is a subset of V x F ...

Not in the bourbaki definition! Only the graph of • is a subset of V x F.

... and this big set also accounts for operations like F x F

How is that? Of course V x F and F x F are different sets (generally).

This is further compounded when thinking of a
group, (G,°), isn't °:G x G → G ? Is (G,°) really (G,G,°) or more explicitly ((G,G),°)?

°:G x G → G means that ° = (G x G, G, F), for some graph F. Thus the group (G,°) = (G,(G x G, G, F)) by substitution.

I just get the feeling that we are creating millions of sets everytime we do something in
mathematics

That's not a problem, this is (rightly) suppressed in understandable well-defined shorthand for the formal set theoretic equivalences. Some may be "sloppy" in their notation, but the rule of thumb is that if you know the set theoretic definitions and understand what is being said, you are perfectly capable of translating back and forth between the two. No one are forcing us to analyze these set theoretic formalities however (but that doesn't make ordinary notation any less rigorous).

If you have further questions you would like a comment on, please try to bold them out and state them separately in a precise manner. Then it is easier for you to know what you want an answer to and easier to answer.

 

[sponsoredwalk]

Great post, it really cleared up a lot & helped me clarify my thoughts, I'll respond to the
quoted bit below & then I have 6 questions in bold with explanatory notes after.

How is that?

In (V,F,((V,V),+),((F,F),+'),((F,F),°),•) I was calling • the set (V,F,•) as a kind of shorthand
but it was just plain stupid. My thinking was that from this big set we could form (V,F,•)
if we chose to since V, F & • are elements of this set. Still though, your response tells
me I was even more wrong calling the set (V,F,•), I should have been calling it
((VxF,F),•)! This is really clarifying! So, to the questions:


1: Would I be more accurate then if I wrote (V,F,((VxV,V),+),((FxF,F),+'),((FxF,F),°),((VxF,F),•))?
as the major set I've been trying to describe?

My thinking is that when we are doing an operation like adding elements of a field we are
working inside ((FxF,F),+'), when we add vectors we're working inside ((VxV,V),+),
when we are scaling up a vector we are working inside ((VxF,F),•) & the set that all
of this is taking place in is (V,F,((VxV,V),+),((FxF,F),+'),((FxF,F),°),((VxF,F),•)).

2: Is a function a set?

All of these things ((FxF,F),°) etc... are functions but I have been working under the
assumption that each of the "functions" in this set are in fact sets, i.e. they are subsets in
which the particular operations are taking place. So for instance, F is in that big set, if I
want to add elements of F it means I am in a set where addition is defined, addition is not
defined in the set F because F is just a set, but this subset ((FxF,F),+') which you're
telling me is a function allows addition as we're just looking at certain ordered pairs &
ascribing our own meaning (addition) to it.

3: Is it a correct assumption to distinguish between sets like ((FxF,F),+') & ((FxF,F),°)?

You see this relates to the idea of these being seperate functions, I think it is fair to call
them distinct sets because if a function is a triple then you need these things to be
distinct. The issue is, are they sets?

4: Is a set with an inner product is distinct from the set I've been illustrating above?

If I were to work in a vector space with an inner product I would have to use a new set
that has this additional set/function ((VxV,F),⊗) so I would have to write the
big set as:
(V,F,((VxV,V),+),((FxF,F),+'),((FxF,F),°),((VxF,F),•),((VxV,F),⊗)).

5: When you write a function like (G x G, G, F), in the domain G x G are there 2 sets G?

I am thinking of a picture like the one I've uploaded as an attachment, in the V x V → V
I am thinking it it the idea everytime you are working with a binary operation. It might be
silly but the cartesian product is always of two sets, it seems justified to me as well
because just as the set {0,0,1} = {0,1} my big set could have two V's, three V's etc...
and it could be written as I have with just one V.

6 Would using the word mapping change any of the concerns I've mentioned above?

Basically I am aware there is some kind of distinction but if it doesn't apply to what I've
described above I wont run into trouble & you needn't worry. I am very used to authors
such as Lang using the words interchangably but have also read there is a distinction.

---

That's it, I don't think I'll have any problems after this (fingers crossed!), really f'ing helpful!

 

[disregardthat]

Ok, I'll see if I can give some reasonable answers to these.. Note that a function is modeled as (X,Y,F), not ((X,Y),F).

1: Would I be more accurate then if I wrote (V,F,((VxV,V),+),((FxF,F),+'),((FxF,F),°),((VxF,F),•))?
as the major set I've been trying to describe?

I assume you are trying to describe a vector space over a field. First, we define our model of a vector space as (abelian group,field,operation), where the operation is a function defining the action of the field on the abelian group. Here we let +,+',° and • be the graphs of the corresponding functions they used to represent to avoid inferring four new symbols. We also let V and F be the sets of vector space elements and field elements respectively.
abelian group = (set, group addition) = (V, (V x V, V, +))
field = (abelian group, multiplication) = ((F, (F x F, F, +')), (F x F, F, °))
operation = (domain, range, graph) = (V x F, V, •)
Hence your vector space may be modeled as
vector space = (abelian group,field,operation) = ((V, (V x V, V, +)), ((F, (F x F, F, +')), (F x F, F, °)), (V x F, V, •)).
Puh.
As you can see, we are not just lotting in the things we want in an arbitrary way, but precisely in the manner we have defined. In this context we can utilize methods in set theory (to extract the elements of our large set) to formally state the properties of the graphs +,+',° and • according to the axioms of abelian groups, fields, vector spaces.

2: Is a function a set?

Well, its model in set theory is. Depending on what you refer to by function, it can either mean it's model (X,Y,F) which is a set and how we can define a function in set theory, or the informal notion of a function as separate from set theory.

3: Is it a correct assumption to distinguish between sets like ((FxF,F),+') & ((FxF,F),°)?

Of course, if the (presumably) graphs +' and ° are different sets then (F x F, F, +') and (F x F, F, °) are not equal as sets. To repeat; yes, they are sets. In one of my previous posts I have referred to the set theoretic definition of a tuple. In particular, any 3-tuple of sets is a set. In general, in set theory, everything is a set!

4: Is a set with an inner product is distinct from the set I've been illustrating above?

Do you mean an inner product space, i.e. a vector space assigned with an inner product? To say an inner product space is equal to a vector space, can mean either that both the underlying vector spaces are equal, or that their respective models in set theory of each is equal. The former may be correct, but the latter is never correct. Indeed, we can choose the definition of a vector space with inner product as the 2-tuple (vector space, inner product) =/= vector space.

(V,F,((VxV,V),+),((FxF,F),+'),((FxF,F),°),((VxF,F),•),((VxV,F),⊗)).

According to my proposal of an inner product space as (vector space, inner product) we would get the following:
vector space = ((V, (V x V, V, +)), ((F, (F x F, F, +')), (F x F, F, °)), (V x F, V, •))
inner product = (VxV, F, ⊗) (Note that ⊗ is the graph of the inner product here)
hence
inner product space = (vector space, inner product)
= (((V, (V x V, V, +)), ((F, (F x F, F, +')), (F x F, F, °)), (V x F, V, •)), (VxV, F, ⊗))
And as before, you will also need to check that ⊗ has the properties of an inner product. Note that the above, regardless of how large it seems, is still a 2-tuple.

5: When you write a function like (G x G, G, F), in the domain G x G are there 2 sets G?

G x G is one set. There is nothing different about defining a function from a cartesian product of two sets than defining it from just a set. The pictures are only intuitional aid.

6 Would using the word mapping change any of the concerns I've mentioned above?

A mapping might mean different things in different contexts, function, continuous function, homomorphism etc.. but my answer would be no.

 

[sponsoredwalk]

I can't tell you how helpful this has been, I haven't been able to do much analysis/linear
algebra because I'd instantly return to this question & then spend all my time looking into
set theory. This model makes perfect sense to me, if I ever have any issues with it I'll be
back but seriously, thanks.

 

[sponsoredwalk]

Note that a function is modeled as (X,Y,F), not ((X,Y),F).

In the pdf file I linked to, http://www.math.bilgi.edu.tr/courses/Lecture%20Notes/SetTheoryLectureNotes.pdf [Broken] ,
page 35, he explicitly says that (X,Y,F) is ((X,Y),F), would this be a case of him using a
different framework?

 

[disregardthat]

In the pdf file I linked to, http://www.math.bilgi.edu.tr/courses/Lecture%20Notes/SetTheoryLectureNotes.pdf [Broken] ,
page 35, he explicitly says that (X,Y,F) is ((X,Y),F), would this be a case of him using a
different framework?

Oh, yes, in some set-theoretical definitions the n-tuples are defined recursively as such: $$(a_1,a_2,...,a_n)=((a_1,...,a_{n-1}),a_n)$$ (with the 0-tuple = the empty set), hence we have set equality between the two. So it doesn't really matter what notation you use. Still, if some other model of tuples were used, such that there would be no such set equality, ((X,Y),F) would be a perfectly adequate model for a function too.

However, this is only the set-theoretical equality of models for functions. In ordinary mathematics I believe we usually consider 2-tuples and 3-tuples necessarily distinct. This convention can of course also be formalized in set theory, by e.g. uniquely indexing the models for the relevant objects (we could for example index tuples by length for the purpose of making the distinct).

 

[sponsoredwalk]

This thread has been extremely helpful over the past few days, I never understood the
example of "The space of functions from a set S to a field F" that's usually given in a
linear algebra text before this. I defined the set as:

((S, (S x S, S, +)), ((F, (F x F, F, +')), (F x F, F, °)), (S x F, F, •)) where:

+ : S x S → S defined by + : (f,g) ↦ (f + g)(x) = f(x) + g(x)
• : S x F → F defined by • : (f,β) ↦ (βf)(x) = βf(x)


I just find it silly writing (f,β) ↦ (βf)(x) = βf(x), can I not write (β,f) ↦ (βf)(x) = βf(x)?
This means I'd write (F x S, F, •), and similarly with the vector space. I don't know if
there's some deep reason underlying the way you've defined it, I have a suspicion but
I thought I'd better ask.

Also, a matrix is a function f : (i,j) ↦ A(i,j) = A_ij. I think the function is more
generally defined as f : F^{m x n} x F^{m x n} → F^{m x n}

To translate it into the set-theoretic language I'm thinking:

((F^{m x n}, (F^{m x n} x F^{m x n}, F^{m x n}, +)), ((F, (F x F, F, +')), (F x F, F, °)), (F^{m x n} x F, F^{m x n}, •))

where

+ : F^{m x n} x F^{m x n} → F^{m x n} defined by + : (i,j) ↦ (A + B)(i,j) = A(i,j) + B(i,j) = A_ij + B_ij

• : F^{m x n} x F → F^{m x n} defined by • : ((i,j),β) ↦ (βA)(i,j) = βA(i,j)

But that seems a bit disconnected. How would I clean that up?