Classical mechanics - sphere attached to rod

[Ene Dene]

Homework Statement

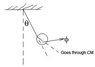
I need to find equations of motion of system on picture. It is easy when one finds Lagrangian so I am not asking you to calculate it, but I'm not sure if I correctly calculated the kinetic energy, so If anyone can verify, I would be greatfull.
The rod has mass m, length 2a, and sphere has mass M, and radius a.

The Attempt at a Solution

The rod:
$$E_{rod}=\frac{1}{2}mv_{CM_{rod}}+\frac{1}{2}I_{rod}\dot{\theta}^2$$
Where I took $$I$$ of rod to be $$\frac{1}{3}m(2a)^2$$, over the edge of rod, not $$\frac{1}{12}m(2a)^2$$, inertia over center of mass of rod.

The same goes for the sphere:
$$E_{sphere}=\frac{1}{2}Mv_{CM_{sphere}}+\frac{1}{2}I_{sphere}\dot{\varphi}^2$$
Where I took moment of intertia over point of connection of rod and sphere. $$I_{sphere}=I_{CM_{sphere}}+Ma^2$$.

Is this correct, or did I missed something?

 

[tim_lou]

for the energy of the rod:

If you use the edge of the rod as fixed point, then you only need the rotational energy of the rod.

If you use the center of mass of the rod, then:
$$T_{\text{rod}}=\frac{1}{2}M\dot{R}_{cm}^2+\frac{1}{2}I_{cm}\dot{\omega}^2$$

same goes for the sphere, if you use the center of mass, then be consistent. find kinetic energy of the motion of the center of mass, then find the rotational energy around the center of mass.

In general, if you use a non-fixed point as the frame in calculating the rotational energy, then you need the kinetic energy of that non-fixed point. It's best to stick with the CM.

if you want the proof:
$$2T=\sum m_i \dot{r_i}^2=\sum m_i \left ( {\dot{r_i}'+\dot{R}}\left )^2=\sum m_i \dot{r_i}'^2+\sum m_i \dot{R}^2+2\sum m_i \dot{R}\bullet\dot{r_i}'$$

if R is defined to be the CM, then the last term goes to zero, thus:
$$2T=\sum m_i \dot{r_i}'^2+\sum m_i \dot{R}_{cm}^2=\sum m_i \dot{r_i}'^2+M \dot{R}_{cm}^2$$

if R is an arbitrary fixed point but not at the CM, then R dot is zero:
$$2T=\sum m_i \dot{r_i}'^2$$

you see, for the rod, you used the pivot as the fixed point, then you should use the third equation, which is simply the rotational energy around the pivot (so, use rotational inertia around the pivot). If you switch to the CM frame, use the second equation (get a term for the kinetic energy around CM, then use the rotational inertia around the CM).

for the sphere, if you use an arbitrary point (connection between the rod and the sphere), then you use the first equation, which involves 3 terms (DO NOT neglect the third term), if you use the cm as the frame of reference, then use the second equations, which has two terms, namely, rotation around the CM and the kinetic energy of the CM.

 

[Ene Dene]

It seems that I wrongly understood theory that solves such problems. Thank you for the explenation. Nevertheless I would like if you could check if I did it correctly:

The rod:
$$E_{rod}=\frac{1}{2}m\dot{r}_{cm}^2+\frac{1}{2}I_{cm}\dot{\theta}^2$$
$$E_{rod}=\frac{1}{2}m(\dot{x}_{cm}^2+\dot{y}_{cm}^2 )+\frac{1}{2}\frac{1}{12}m(2a)^2\dot{\theta}^2$$
$$x_{cm}=a\cdot{sin\theta} \Rightarrow \dot{x}_{cm}=a\cdot{cos\theta}\cdot{\dot{\theta}}$$
$$y_{cm}=a\cdot{cos\theta} \Rightarrow \dot{y}_{cm}=-a\cdot{sin\theta}\cdot{\dot{\theta}}$$
$$E_{rod}=\frac{2}{3}ma^2\dot{\theta^2}$$

I get the same result if I take fixed edge of rod, and for translation take 0(edge is not moving), just as you said:

$$E_{rod}=\frac{1}{2}\frac{1}{3}(2a)^2m\dot{\theta}^ 2=\frac{2}{3}ma^2\dot{\theta^2}$$

And now, here is a sphere:

$$E_{sphere}=\frac{1}{2}M\dot{r}_{cm}^2+\frac{1}{2}I_{cm}({\dot{\theta}+\dot{\phi}})^2$$
$$E_{sphere}=\frac{1}{2}M(\dot{x}_{cm}^2+\dot{y}_{cm}^2)+\frac{1}{2}\frac{2}{5}Ma^2({\dot{\theta}+\dot{\phi}})^2$$
where:
$$x_{cm}=2a\cdot{sin\theta}+a\cdot{sin(\theta+\phi)$$
$$y_{cm}=2a\cdot{cos\theta}+a\cdot{cos(\theta+\phi)$$
etc.

Is this correct kinetic energy for sphere?

 

[tim_lou]

i don't think the phi dot should be in the rotational energy of the sphere. pretend you are in the frame of the sphere. the rotation of the sphere depends solely on phi dot.

other than that, the equation looks good.