- #1
Nubcakes
- 7
- 0
So I've never gotten a straight answer as to how you calculate the resistance of a coil (or cap for that matter). I hesitate to use the term "impedance" because I've been told too many times to count that impedance is the total resistance of a circuit. My professors dance around the topic from time to time but they have never given me a straight answer. I've talked to practicing electrical engineers where I work(as an intern) and they give me the deer in the headlights look. Eventually they all cough up the reactance formula. The only other response I've gotten from an RF-engineer was to use this formula: Z = SQ(r^2 + X^2). X is reactance. I've taken it all for granted until one of my friends today told me neither works in real life.
So I decided to get some components and built up an RL circuit to see what actually happens. I used multiple relatively accurate meters to measure the values within the circuit. All meters gave me the same results within 5% so I am pretty sure the measured values are correct. Below is the circuit and calculations I did;
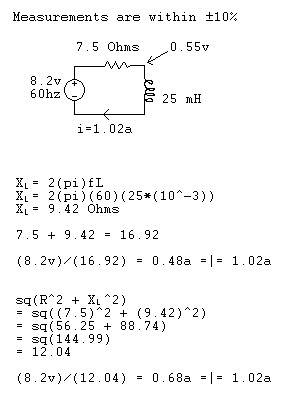
Neither formula gives the correct resistance of the coil. According to my actual test the resistance of the coil at 60Hz should be 0.54 Ohms. Can anyone help me figure this out? Thanks!
EDIT: Just to be clear, this is not for a class in anyway shape or form. This is strictly for my personal understanding.
So I decided to get some components and built up an RL circuit to see what actually happens. I used multiple relatively accurate meters to measure the values within the circuit. All meters gave me the same results within 5% so I am pretty sure the measured values are correct. Below is the circuit and calculations I did;
Neither formula gives the correct resistance of the coil. According to my actual test the resistance of the coil at 60Hz should be 0.54 Ohms. Can anyone help me figure this out? Thanks!
EDIT: Just to be clear, this is not for a class in anyway shape or form. This is strictly for my personal understanding.
Last edited: