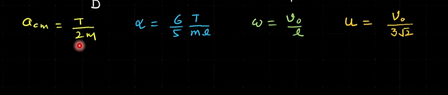Collision of a bullet on a rod-string system: query

[palaphys]

Homework Statement

In attachment below

Relevant Equations

Tau= I alpha, L= rxp

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question.

Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point?
Lets call the point which connects the string and rod as P.
Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string acting as a constraint. Also, it is clear from intuition that the rod will aquire an angular velocity in an anticlockwise manner just after the collision. Hence, the point P has a radial acceleration, as well as centripetal acceleration, with respect to the ground frame.

Does that mean, when observed from the frame of P, there must be a PSEUDO force on the center of mass, and hence, angular momentum is NOT conserved about that point?

But the solution to this question seems to suggest otherwise.

Please help.

 

[palaphys]

All relevant attachments are below, for those who need the solution/ question statement

 

[PeroK]

A pseudoforce is only relevant if you want to analyse the problem in an accelerating reference frame. In general, different quantities are conserved in an accelerating reference frame compared to an inertial reference frame - because of the additional pseudoforce.

 

[haruspex]

There is an instantaneous impulse from the string. This has no moment about P, so does not affect angular momentum about P.
But note that "P" is ambiguous here. Does it mean a fixed point in the rest frame or does it mean wherever that end of the rod is at any point in time? In calculating angular momentum, this can matter. It is safe to use fixed points.

 

[palaphys]

There is an instantaneous impulse from the string. This has no moment about P, so does not affect angular momentum about P.
But note that "P" is ambiguous here. Does it mean a fixed point in the rest frame or does it mean wherever that end of the rod is at any point in time? In calculating angular momentum, this can matter. It is safe to use fixed points.

A pseudoforce is only relevant if you want to analyse the problem in an accelerating reference frame. In general, different quantities are conserved in an accelerating reference frame compared to an inertial reference frame - because of the additional pseudoforce.

Well I am considering the angular momentum about point P.
Case 1: what would happen if I considered the angular momentum about the point P on the rod?
Case 2: is it possible to consider the angular momentum about some other point which is probably fixed to the GROUND, but coincides with P? Is that ''legal'' ? Because it does not feel right to me

 

[PeroK]

Well I am considering the angular momentum about point P.
Case 1: what would happen if I considered the angular momentum about the point P on the rod?
Case 2: is it possible to consider the angular momentum about some other point which is probably fixed to the GROUND, but coincides with P? Is that ''legal'' ? Because it does not feel right to me

I think @haruspex identified the source of your confusion. In any case, it all depends whether you transform to an accelerating reference frame or not. Choosing a different point (in space) for an instantaneous analysis does not do that. Of course, if you follow a point on the rod as it moves and keep this as the origin over time, then you are using an accelerating reference frame.

 

[palaphys]

I think @haruspex identified the source of your confusion. In any case, it all depends whether you transform to an accelerating reference frame or not. Choosing a different point (in space) for an instantaneous analysis does not do that. Of course, if you follow a point on the rod as it moves and keep this as the origin over time, then you are using an accelerating reference frame.

I want to keep it as simple as possible, but I want to know what the difference would be, when I consider a material point on a body vs point on ground (space)

 

[PeroK]

I want to keep it as simple as possible, but I want to know what the difference would be, when I consider a material point on a body vs point on ground (space)

A point on a body, used as the origin over time, might imply an accelerating reference frame. Newton's laws (without the addition of pseduo-forces) demand an inertial reference frame.

 

[palaphys]

A point on a body, used as the origin over time, might imply an accelerating reference frame. Newton's laws (without the addition of pseduo-forces) demand an inertial reference frame.

My main question is that how can I conserve angular momentum about P??? The solution some how includes this. But it has not specified which point P is (whether on the rod or on the ground)

 

[PeroK]

My main question is that how can I conserve angular momentum about P??? The solution some how includes this. But it has not specified which point P is (whether on the rod or on the ground)

P is taken to be a fixed point. Or, more accurately, the solution assumes we are working in the inertial reference frame where the ground remains at rest.

 

[haruspex]

Btw, I would not bother finding the CM or its velocity or moment of inertia. It is simpler to find the momentum and angular momentum of each mass separately then sum as appropriate.

 

[palaphys]

Btw, I would not bother finding the CM or its velocity or moment of inertia. It is simpler to find the momentum and angular momentum of each mass separately then sum as appropriate.

But here in the question, it seems that it is unsolvable without finding the MOI, velocity of cm etc.

 

[palaphys]

P is taken to be a fixed point. Or, more accurately, the solution assumes we are working in the inertial reference frame where the ground remains at rest.

Okay, I am clear now. thanks

 

[palaphys]

I was going through the solution once more, and yet another thing struck me: in the solution, both alpha and Omega are given a +ve sign. How is this correct? Aren't the angular acceleration and angular velocity in opposite directions?? In the attatchment below, I have considered alpha and Omega to have the same signs. However aren't they in opposite (i.e alpha is clockwise and Omega is anticlockwise?)

 

[PeroK]

I was going through the solution once more, and yet another thing struck me: in the solution, both alpha and Omega are given a +ve sign. How is this correct? Aren't the angular acceleration and angular velocity in opposite directions??

If an object starts at rest, then the velocity just after an impact must be in the direction of the initial acceleration/impulse.

 

[palaphys]

If an object starts at rest, then the velocity just after an impact must be in the direction of the initial acceleration/impulse.

That sounds intuitive, but torque analysis about the CM using right hand rule tells me that angular acceleration is in the clockwise direction, and intuition tells me the rod will rotate anticlockwise, and Omega is in that direction as well ( dtheta/dt)

 

[PeroK]

That sounds intuitive, but torque analysis about the CM using right hand rule tells me that angular acceleration is in the clockwise direction, and intuition tells me the rod will rotate anticlockwise, and Omega is in that direction as well ( dtheta/dt)

If the initial angular acceleration is $\alpha(0)$, then the angular velocity after a small time interval is approximately $\omega(\Delta t) \approx \alpha(0) \Delta t$.

 

[Lnewqban]

That sounds intuitive, but torque analysis about the CM using right hand rule tells me that angular acceleration is in the clockwise direction, and intuition tells me the rod will rotate anticlockwise, and Omega is in that direction as well ( dtheta/dt)

Without the attached string, how the rotation would happen?

 

[palaphys]

Without the attached string, how the rotation would happen?

Anticlockwise. But how is that going to help?

 

[palaphys]

If the initial angular acceleration is $\alpha(0)$, then the angular velocity after a small time interval is approximately $\omega(\Delta t) \approx \alpha(0) \Delta t$.

But, I thought when solving problems we use a proper sign convention..

 

[PeroK]

But, I thought when solving problems we use a proper sign convention..

The sign convention doesn't matter. Initial acceleration and "Initial" velocity are in the same direction.

That only applies when starting from rest, of course.

 

[kuruman]

But, I thought when solving problems we use a proper sign convention..

You thought correctly. Nevertheless, ask yourself the question "If a rod, initially at rest, is given an angular acceleration $\alpha(0)$, will its angular velocity not be in the same direction as the angular acceleration but will depend on the choice of "proper" sign convention?" Nature does not follow human conventions.

 

[PeroK]

The sign convention doesn't matter. Initial acceleration and "Initial" velocity are in the same direction.

That only applies when starting from rest, of course.

Okay, I see that the initial angular velocity might be non-zero in this case and the rotation immediately slowing down.

 

[palaphys]

You thought correctly. Nevertheless, ask yourself the question "If a rod, initially at rest, is given an angular acceleration $\alpha(0)$, will its angular velocity not be in the same direction as the angular acceleration but will depend on the choice of "proper" sign convention?" Nature does not follow human conventions.

Yes, I see it now. It seems rather senseless to assign angular acceleration and angular velocity opposite directions here, especially as the rod is starting from rest.

 

[palaphys]

Alright got it, everything is clear now.

 

[haruspex]

But here in the question, it seems that it is unsolvable without finding the MOI, velocity of cm etc.

Not so. Pretty much the only time you need to find the CM of an assembly is when you are asked for something specifically related to that, such as its position, velocity, etc.

 

[Lnewqban]

Anticlockwise.

How and why does the string interfere with that rotation?

 

[WWGD]

A Rod? I thought he had retired. Ask @Charles Link , he's the main Baseball guy here.

 

[Charles Link]

A Rod? I thought he had retired. Ask @Charles Link , he's the main Baseball guy here.

Yesterday, with @WWGD mentioning me, was the first look that I had at this thread. I read the problem in the OP, but I don't want to look at any solutions that have been posted in the thread until after I spend at least a little time trying to solve it myself. From my first impressions of it, it looks like the string supplies both an impulse $\Delta(mv)= \int F \, dt$ along with a very short $\Delta L= \int \tau \, dt$, (for which $T$ can't be computed, but rather $\int T \, dt$), after which there is likely to be a tension $T$ supplying a centripetal force, but this looks to me to be a somewhat non-trivial problem, and it might take me a day or two or longer to come up with a solution. It looks very interesting though.

 

[Charles Link]

I now have a preliminary solution to the problem posed in the OP. I think you can make the assumption that the string can stretch a small amount before it has any effect, so that the rod can be treated as a free object for the initial impact. The rod/bullet system will thereby have an initial velocity of its center of mass, along with an angular velocity about its center of mass. It is then that the string will come into play, exerting an impulse of $\int T \, dt$ which has vector components that will cause a momentum change and thereby a change in the center of mass velocity, as well as a change in the angular momentum from the torque, and thereby a change in the rotational rate about the center of mass. The impulse $\int T \, dt$ must result in the velocity of the attachment point to be zero in the direction of the string.

Preliminary results are that the moment of inertia $I=(5/24)mL^2$, and after some lengthy calculations $\int T \, dt=4 mv_o \cos(\theta)/(27 \cos^2(\theta)+5)$.

I will try to post more detail over the next day or two. I also anticipate I may have some algebraic errors.

One additional comment is that right after this impulsive $\int T \, dt$, one could anticipate that the tension in the string is near zero because the velocity of the point of attachment along the string is zero.

Edit: It may also be worth mentioning that the torque=rate of change of angular momentum applies to either a stationary point as the origin, but also holds when referenced about the center of mass, even if the center of mass is undergoing an acceleration.