Column buckling answer confirmation

[charger9198]

https://www.physicsforums.com/attachments/42439

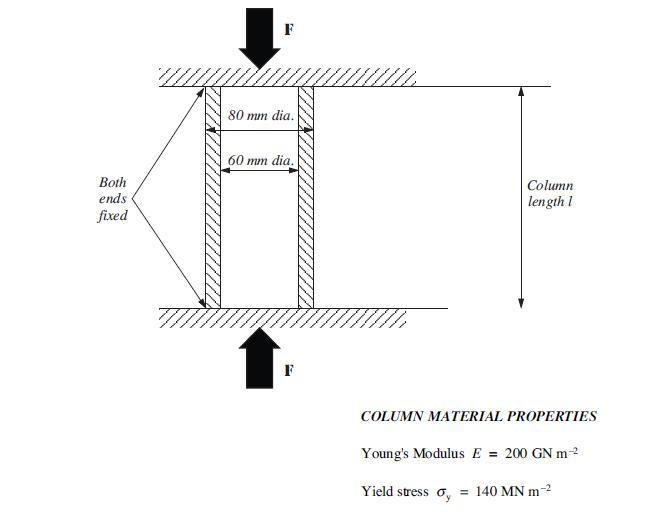
What is the minimum length of the column at which buckling is likely to occur?


The buckling equation is: F= ((∏^2)*E*I)/(K*L)^2

E is the modulus, I is the area moment of inertia, K is the buckling coefficient, and L is the length of the column.

the mass moment of inertia for a hollow tube is;

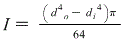
(using meters)

I = (0.08^4-0.06^4)∏/64 = 1.37 x 10^-6 m^4


for the force, F, that will cause yielding.

The equation is:

σ= F/A

The cross sectional area of the column is:

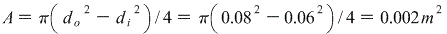
Need to convert MN/m^2 to GN/m^2 by multiplying by 10^-3.

Therefore, F = Aσ = 0.02 x 141 x 10^-3 = 3.08x10-4 GN

The value of K for fixed-fixed end conditions is 0.5

Therefore, rearange the equation and solve for L


L= (SQRT) ((∏^2)*E*I)/F*k^2 = 5.93 m

This means, if the column is longer than 5.93 meters, it will buckle due to slenderness. Otherwise, if it is shorter than 5.93 meters, it will not displace out of plane and fail in yielding.

 

[nvn]

charger9198: MN/m^2 is called MPa. And GN/m^2 is called GPa. Always use the correct, special name for a unit. E.g., 140 MPa, not 140 MN/m^2.

If you have written the problem statement in post 1 exactly as given, then it might indicate the instructor has a limited understanding of buckling, because the question is unclear. A column can buckle at almost any length, if the applied load is high enough (i.e., as we move toward, and into, the inelastic range). The question would be more clear if it were instead worded as follows. "What is the minimum length of the column at which elastic buckling is likely to occur?"

Currently, the best assumption is to assume the word "elastic" was intended to be inserted by the instructor. Also, we might assume the instructor wants you to pretend the column is theoretically perfectly straight.

Therefore, using these assumptions, your current answer, 5.93 m, is correct, or close to correct. (You rounded numbers in your intermediate calculations too much. If you had maintained at least four significant digits throughout all your calculations, which you should have done, then you would have obtained 5.94 m.) Also, you should use 140 MPa, not 141 MPa.

 

[charger9198]

Nvn: thanks I've altered to suit and I used all the numbers without rounding to come up with 5.94.

The question given was exactly as wrote.

To go with the question I got asked 'what will be the mode of failure' which I got as buckling

The question after that asked 'at what load would you expect the failure to occur'

I used the equation (Pi^2)*E*I/(K*L)^2
=
(Pi^2)*200*1.374x10^-6/(0.5*5.94)^2
Giving me 3.07 x 10^-4 GPa

 

[nvn]

charger9198: Once again, you rounded your numbers too much; therefore, your answer is slightly inaccurate. And your units are wrong. GPa is a unit of pressure or stress, not force.

 

[charger9198]

Thanks nvn I have re wrote the full thing using the full answers and it looks a lot more clear now..

F=3.07875 x 10^-6

 

[nvn]

charger9198: Generally always maintain at least four significant digits throughout all your intermediate calculations, then round only the final answer to three significant digits, unless the first significant digit of the final answer is 1, in which case round the final answer to four significant digits.

Therefore, your final answer in post 5 should be rounded to three significant digits. You listed six significant digits in your final answer in post 5.

Also, your power (exponent) in post 5 is wrong. And no units are listed.

 

[charger9198]

nvn: Thanks;

F = 3.078 x 10^-4 GN

 

[nvn]

charger9198: It appears you might not know how to round numbers. When rounding numbers, 0 to less than 5 is truncated; 5 to 9 is rounded to the next higher digit.

E.g., 3.07875, rounded to four significant digits, is 3.079, not 3.078. Or, 3.07875, rounded to three significant digits, is 3.08.

Therefore, your final answer would be F = 3.08 x 10^-4 GN.

However, it is probably clearer to instead write 0.308e-3 GN, or 308e3 N, or 308 000 N, or 308 kN.

Here are some other, easier ways you can write the same number; 3.08e-4 GN, 0.308e-3 GN, 0.308 MN, 308 kN, 308e3 N, 0.308e6 N, 308 000 N.

 

[pongo38]

Charger: you wrote "This means, if the column is longer than 5.93 meters, it will buckle due to slenderness. Otherwise, if it is shorter than 5.93 meters, it will not displace out of plane and fail in yielding."

Columns under load can displace out of plane without it being buckling. The test is whether on removal of the load, the column returns to its original position. One definition of buckling load is: If you displace the loaded column with a perturbation and it remains displaced, then it has buckled. NVN's advice is always good, but just don't believe that the results of the calculation are true to the number of significant figures you are using. In my experience you would be lucky if two sig figs were to correctly predict a column buckling load, there being very many variables that the theory ignores.

 

[charger9198]

Thanks for all the help Pongo38 and NVN. chemistry is more of my field but my basic math principles are far from adequate. I'm trying to take all advice on board and apply to successfully gain better physics knowledge..thanks again

 

[Nobby3601]

I am using the formula L= (SQRT) ((∏^2)*E*I)/F*k^2 and not coming out with anything like this answer. Would you mind breaking it down?

Thanks

 

[nvn]

Nobby3601: You must use consistent units. Consistent units are, e.g., N, m, Pa.

 

[Nobby3601]

Thanks for the help all. Got there in the end!

 

[Carlo2986]

Your answer to 'At what load would you expect failure to occur?', Could'nt you have used the equation:

F_c = σ_cA

F_c being the axial load
σ_c being the critical stress which will cause buckling
A being the cross section area

It gives the same answer and is a lot shorter.

Or is it not as easy as that?

 

[Rafeng404]

Hi all, I also have this question as part of my assignment and I was getting a different answer.. I was wondering how you know what shape the column is from the question? You can get rectangular columns too, can't you? :/

 

[SteamKing]

The dimensions from the problem statement attachment list '80 mm dia.' for the outer dimension and '60 mm dia.' for the inner dimension. 'dia.' or diameter implies a circle rather than a square or rectangle.

 

[Rafeng404]

So basically I need to be an English professor as well as an engineer to get this HNC... Haha. Thank you for your fast response, much appreciated.

 

[Rafeng404]

Hello again, I have don't all ,y calculations and I have got the same as everyone else.. I am doing this distance learning and the books aren't very good. I'm struggling to see what values I should be comparing to determine what the mode of failure would be, ie if its buckling how have I proved it mathematically..

Not sure what all this has to to with electrical and electronic engineering!,, rant over haha.

 

[Rafeng404]

*Done all the

 

[forexpipz]

I'm almost certain that the column length is 5.236389088 m.

 

[forexpipz]

Disregard my last post. I used the wrong formula for A and K. Now I am on it. Its around 5.9 m off the top of my head.

 

[mamike1515]

Hi All
I have just looked at this problem and just wanted to confirm my answer, which is different to everyone else!
The question stated the diameters of 80mm and 60mm with E = 200GNm^2 and σ = 140MNm^2

To calculate the minimum length of the column at which buckling is likely to occur

ESR = L/k, so L = ESR x k

ESR = √pi^2 x E / σ

ESR = 118.74k = √I/A with I = pi( R^4 –r^4) / 4 and A = pi( R^2 –r^2)
With R = 40mm and r = 30mm

k = 0.025mWhich gives the minimum length as 2.97m (118.74 x 0.025m)

 

[SteamKing]

Hi All
I have just looked at this problem and just wanted to confirm my answer, which is different to everyone else!
The question stated the diameters of 80mm and 60mm with E = 200GNm^2 and σ = 140MNm^2

To calculate the minimum length of the column at which buckling is likely to occur

ESR = L/k, so L = ESR x k

ESR = √pi^2 x E / σ

ESR = 118.74


k = √I/A with I = pi( R^4 –r^4) / 4 and A = pi( R^2 –r^2)
With R = 40mm and r = 30mm

k = 0.025m


Which gives the minimum length as 2.97m (118.74 x 0.025m)

The slenderness ratio L/r uses the effective length of the column, instead of the actual length. The effective length is determined by the support conditions at the end of the column. For a fixed-fixed column, the theoretical effective length is equal to half of the length between supports.

 

[mamike1515]

Thanks Steamking.
Looks like I missed the column design notes!

So Le=L/2
L=Le x 2
L=2.97m x 2 = 5.94m, which is the minimum length of the column at which buckling is likely to occur.

 

[kampftrimker]

Hi, I'm currently doing this question and am a little stuck on the last question.

Answers i have already are as follows: (I'm happy with these)
1. What is the minimun length of the column at which buckling is likely to occur
ANS = 5.937 m

2. If the column is the length determined in the last question what would be the mode of failure
ANS = Buckling

3. At what load would you expect failure to occur
ANS = 3.078 x 10^5 N

4. If the column is half the the length determined in question 1 what would be the mode of failure.
ANS = Crushing (i'm assuming this as the minimum length for buckling is 5.937 so anything less must be crushing

This next one is the one I'm struggling with

5. At what load would yo expect failure to occur.

I don't need the answer, just pointing in the right direction. I'm assuming it isn't as simple as
F = σ * A

Thanks for reading.

 

[mamike1515]

You are on the right track by using Eulers equation and the question is asking what load would the failure occur?

Remember Eulers Equation isn't just Fc=σ*A it is also pi^2*EI / Le^2.

Also remember that the column is fixed at both ends

 

[kampftrimker]

Thanks for your reply,

if I use pi^2*EI / Le^2 I get a fiqure of 1.231 x 10^6 N

This is just using the same formula i used for Q3 but I halved the length.

If I've got it right great, I was just expecting something more complicated for some reason.

 

[mamike1515]

Kampftrimker, it looks fine to me.

Basically halving the length of the column increases the load failure by approx 4 times

 

[kampftrimker]

Thanks for that, i was under the impression that the pi^2*EI / Le^2 formula was only for buckling stress.

 

[adamhere]

For part two "What would the mode of failure be?"
How did you prove it would be buckling?

 

[kampftrimker]

Hi Adam,

My answer to that was only half right, the mode of failure could be either, as the length is the minimum length at which buckling will occur.

Mick

 

[mamike1515]

Hi Adam

Have a look at the Effective Slenderness Ratio values, which determine whether crushing or buckling is the main cause of column failure.

 

[adamhere]

Thanks for the quick replies
I have the Effective Slenderness Ratio as 118.74. Am I supposed to have another value to compare to this?
Maybe by changing the yield stress value for the critical stress value? So I would get a higher ESR (Worked out as 2532.04) which would indicate Buckling.
Is this along the right lines?

 

[mamike1515]

Hi Adam
Looks like you have arrived at the correct ESR figure (118.74). Basically the minimum E.S.R. for which buckling occurs, is the one when the critical stress σc equal to the yield stress of the material σy. For a mild steel with E = 200 GPa and σc = σy = 240 MPa, the slenderness ratio is about 91.
That means when effective slenderness ratios are less than 91, crushing is the failure mode, for values above 91 buckling is the mode. Hope this helps!

 

[Gavin Cooper]

Nvn: thanks I've altered to suit and I used all the numbers without rounding to come up with 5.94.

The question given was exactly as wrote.

To go with the question I got asked 'what will be the mode of failure' which I got as buckling

The question after that asked 'at what load would you expect the failure to occur'

I used the equation (Pi^2)*E*I/(K*L)^2
=
(Pi^2)*200*1.374x10^-6/(0.5*5.94)^2
Giving me 3.07 x 10^-4 GPa

can someone explain what units you are supposed to use?
Is putting 200 into the equation correct as it is 200GNm-2.
I am confused

 

[Gavin Cooper]

Nvn: thanks I've altered to suit and I used all the numbers without rounding to come up with 5.94.

The question given was exactly as wrote.

To go with the question I got asked 'what will be the mode of failure' which I got as buckling

The question after that asked 'at what load would you expect the failure to occur'

I used the equation (Pi^2)*E*I/(K*L)^2
=
(Pi^2)*200*1.374x10^-6/(0.5*5.94)^2
Giving me 3.07 x 10^-4 GPa

 

[SteamKing]

can someone explain what units you are supposed to use?
Is putting 200 into the equation correct as it is 200GNm-2.
I am confused

Remember, G = * 10^9. You want to express all quantities with K, M, or G, or m, or c in terms of their numeric values multiplied by the value of these unit prefixes.

 

[Gavin Cooper]

Steam king Thanks for the reply, when using Eulers equation does it matter what units you use, should E be GNm-2 and I be Meters, or E be Nm-2 an I be mm, just not quite got my head round this bit.

 

[SteamKing]

Steam king Thanks for the reply, when using Eulers equation does it matter what units you use, should E be GNm-2 and I be Meters, or E be Nm-2 an I be mm, just not quite got my head round this bit.

Yes, it does matter which units you use, not only for Euler's formula, but for any formula. No, you can't throw a bunch of different units into a formula and expect things to sort themselves out properly.

It sounds like you have some basic misconceptions about applying units, especially those in SI.

Take, for example, a very simple formula, like the area of a rectangle, A = b * h. If I have measured the breadth in kilometers and the height in centimeters, I can't simply multiply these two different measurements together and expect the area to come out in square meters. If I want to calculate an area measured in square meters using the formula A = b * h, then the measurements of b and h must be converted to meters before I plug them into the formula. Failing this, then I have to calculate a conversion factor to determine how many kilometer-centimeters are in 1 square meter.

 

[Gavin Cooper]

Thanks Steam Kining, think I've got it, just didn't read things correctly.
My last problem is that I've worked ot the SR to a colulumn as being equal to the ESR. My notes do not tell me how the column would fail in a case like this. Is there any other equation I should be looking at to find this answer.

 

[Gavin Cooper]

Thanks Steam Kining, think I've got it, just didn't read things correctly.
My last problem is that I've worked ot the SR to a colulumn as being equal to the ESR. My notes do not tell me how the column would fail in a case like this. Is there any other equation I should be looking at to find this answer.

Disregard this comment. I know what I done wrong. Doh!

 

[js3]

Good afternoon, i am working on the same assignment and I'm having a couple of issues. Any help would be greatly appreciated.
To calculate to load i would expect failure at the first length(5.92m), my numbers are as follows:

F= Pi^2*200*(1.37*10^-6)/2.96^2
F=3.087*10^-4
Firstly, could somebody confirm whether this is in GN? The reason i ask is because the value i put in for E is 200GNm^-2.

With regard to the next question, i saw that mamike wrote 'Basically halving the length of the column increases the load failure by approx 4 times'

My calculation suggests otherwise:
F=Pi^2*200*(1.37*10^-6)/1.48^2
F= 1.234*10^-3

Lastly, with regard to finding the mode of failure.
I have calculated the ESR, and achieved 118.74 like everybody else. Now when i calculate the S.R. i get the same again (using SR=Le/k).
Gavin cooper was having the same issue, but found the solution and didn't share it.
There is nothing in my material to suggest how i can calculate this. Frustrating.
Thanks in advance.

 

[SteamKing]

To calculate to load i would expect failure at the first length(5.92m), my numbers are as follows:

F= Pi^2*200*(1.37*10^-6)/2.96^2
F=3.087*10^-4

With regard to the next question, i saw that mamike wrote 'Basically halving the length of the column increases the load failure by approx 4 times'

My calculation suggests otherwise:
F=Pi^2*200*(1.37*10^-6)/1.48^2
F= 1.234*10^-3

If F = 3.087×10^-4, then what do you calculate for 4*F ? Compare with 1.234×10^-3.

 

[js3]

If F = 3.087×10^-4, then what do you calculate for 4*F ? Compare with 1.234×10^-3.

*hides red face* Haha thanks for that, i'll never know how i didn't see that...
As for units, am i correct in thinking we are talking gigaNewtons?
Thanks again.

 

[SteamKing]

*hides red face* Haha thanks for that, i'll never know how i didn't see that...
As for units, am i correct in thinking we are talking gigaNewtons?
Thanks again.

The units of F appear to be gigaNewtons.

 

[js3]

Much appreciated. Thanks for your help steam king.
I just need to try and get my head around how to decide whether the column will fail by buckling or yielding.
I don't understand the way it is worded in my notes. It does not seem to give a calculation for which you can determine the type of failure.

 

[cjm181]

Hi
Js3, did you get the answer to the last part of your post above. I am also struggling here.
If I have this right, we need to find the SR of our tube. Then if the ESR is less than that, then the failure is crushing, if its more then the failure is buckling. Is that right?

I get the ESR to 118.74, but get the SR to 449.02. So I guess I have done something wrong here? As we have just calculated the minimum length at which buckling can occur, then I would expect the ESR and SR to be close (if not the same). Using my theory above it would suggest the failure is crushing. It does not add up to me

for SR, I used L/k.
k=(1/2)√((R²-r²)=0.5 x √(0.04²-0.03²) = 0.013229

so SR=5.94/0.013229=449.02

Kr
C

 

[SteamKing]

Hi
Js3, did you get the answer to the last part of your post above. I am also struggling here.
If I have this right, we need to find the SR of our tube. Then if the ESR is less than that, then the failure is crushing, if its more then the failure is buckling. Is that right?

I get the ESR to 118.74, but get the SR to 449.02. So I guess I have done something wrong here? As we have just calculated the minimum length at which buckling can occur, then I would expect the ESR and SR to be close (if not the same). Using my theory above it would suggest the failure is crushing. It does not add up to me

for SR, I used L/k.
k=(1/2)√((R²-r²)=0.5 x √(0.04²-0.03²) = 0.013229

so SR=5.94/0.013229=449.02

Kr
C

cjm181:
The policy at PF is not to encourage posting to old threads, also called necroposting. The member you are trying to engage has moved on and not posted anything in 6 months or so.

If you have a specific question about a problem, create your own thread. You can always refer to other threads at PF for clarity.