Combination of capacitors

[Abhimessi10]

Homework Statement

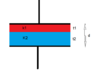
Between the plates of parallel plate condenser having charge Q,a plate of thickness t1 and dielectric constant k1 is placed.In the rest of the space,there is another plate of thickness t2 and dielectric constant K2.The potential difference across the condenser will be.

Homework Equations

C=kAe0/(d-t+t/k)
k----->dielectric constant
A--->Area of the plates
e0---->permittivity
d---->distance between the plates
t------>thickness of the plate

V=Qnet/C

The Attempt at a Solution

Combination of capacitors with materials of dielectric constant K1 and K2 is obtained.i am not sure if this parallel or series connection.

My logic says they are in series.

So Cnet=C1C2/C1+C2

But i am not arriving at a final answer

[/B]

 

[kuruman]

Your logic is correct, they are in series. Also your formula for the equivalent capacitance is correct. So now what are C1 and C2?

 

[Abhimessi10]

Your logic is correct, they are in series. Also your formula for the equivalent capacitance is correct. So now what are C1 and C2?

Yeah but isn't the distance between the plates of C1 d/2 ?

 

[Merlin3189]

Yeah but isn't the distance between the plates of C1 d/2 ?

Not on my reading of the Q.

... ,a plate of thickness t1 and dielectric constant k1 is placed. In the rest of the space,there is another plate of thickness t2 and ...
d---->distance between the plates
t------>thickness of the plate

the dielectric plates are thickness t1 and t2 and they filled the gap d between the plates, so that t1 + t2 = d
It is not stated that t1 = t2

 

[Nik_2213]

IMHO, the question is both incomplete and ambiguous but, given the information provided, can only be solved as 'C in Series'.

 

[Abhimessi10]

IMHO, the question is both incomplete and ambiguous but, given the information provided, can only be solved as 'C in Series'.

Is there any combination in which the area of both plates become A/2(not related to this question)

 

[kuruman]

You can have the gap in the bottom half of the capacitor be completely filled with one kind of dielectric and the top half filled with a different kind. Is that what you mean? (Not the case here).

 

[Merlin3189]

You can have the gap in the bottom half of the capacitor be completely filled with one kind of dielectric and the top half filled with a different kind. Is that what you mean? (Not the case here).

I thought that's exactly what we have here? EDIT: Except that it's not halves

 

[kuruman]

I thought that's exactly what we have here? EDIT: Except that it's not halves
View attachment 230773

That's exactly my interpretation.

 

[gneill]

Is there any combination in which the area of both plates become A/2(not related to this question)

Only if the dielectric slabs are arranged side by side and so divide the plate area between them. The width of the dielectrics would have to be identical in order to divide the area of the plates equally.

In this case you could consider the resulting device to be two capacitors with the same plate area (A/2) but different dielectrics and connected in parallel.