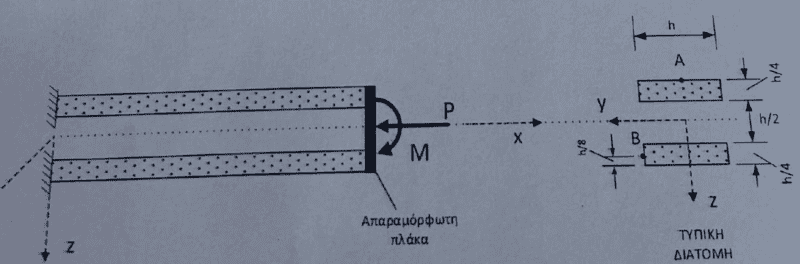
Because the beam is fixed at the left side and it's held together by an undeformable plate at the right side you can solve the problem as a typical beam. Just with a little special-looking cross-section. You could imagine this beam being a ##I## profile where the web is just very thin but somehow the cross section is held together.
It's often useful to divide the acting forces and later add them back together to get the full picture. There are a few conditions that must be met for this to be possible but there's no point in discussing that now.
Acting moment M.
Since the cross-section is symmetric and the material of both beams is the same, the neutral axis will be in the center. It might look weird that it falls in an empty area but it's possible because of the plates fixed at both ends. It's similar to the center of mass of an empty circle that will be at a point where there is no mass.
The actual neutral line will be displaced due to the compression acting but we'll see that later when we add the effects of the two forces.
From your diagram, the neutral line is at ##z=0##.
Here is some additional reading for the neutral axis
(notice the book didn't use the same coordinates as your problem).
MECHANICS OF MATERIALS
BARRY J. GOONO / JAMES M. GERE
Secondly, the moment of inertia of the section will be ##\int_{A}z^2dA##. Since they are just two blocks, you can either use the parallel axis theorem
@erobz mentioned in #7 or you can subtract the moment of the empty cross-section from the full cross-section kind of how you would do it to find the area of that surface. I checked it for this area and it gives the same result (##\frac{7}{96}H^4##) using both methods. However, I'm not certain if that's just a coincidence because of all the symmetries in that cross-section or if it's a general result. Maybe
@erobz knows more about that. If we can't find a confirmation, I'd proceed with the parallel axis theorem for general cases as he suggested.
Now that the neutral line's position, moment of inertia of the cross-section, and acting moment are known it is then possible to find the stress $$\sigma_x(z)=-\frac{M_yz}{I_y}$$ where ##M>0## so for ##z<0## (above the neutral line from your picture) the normal stress is positive (causing tensions).
Tension is 0 where there is no material. I used 00 to indicate that there is no tension because there is no material and that's also the neutral line that would be coming out of the screen.Acting force P
For the compression caused by ##P##, it's much simpler. It'll just be the acting force divided by the total area so it'll be
$$\sigma_x=\frac{P}{A}$$ where ##P## is negative.
Finally, it's necessary to check the total effect of the combination of both.
Which gives the same "shape" but it is displaced due to the effect from ##P##. As you can see, that displaces the neutral line. That will result in the lower side of the composed beam failing first because both ##M## and ##P## are causing compression on it.
Curiously enough, for materials that behave similarly in compression and tension (things like metals for example that are considered when starting these subjects) adding ##P## always has a negative impact. However, there are materials that are awful at resisting tension but are pretty good at resisting compression (concrete is the most common example). For those materials, you can see how the effect from ##P## can be positive in that scenario because the tension is reduced and the increment in compression can be resisted by the material.
Cycling loads can be another example where ##P## could be beneficial and I'm sure there are many more but those are the ones that came to my mind now.